Предмет: Математика,
автор: adigineevk2
интеграл помогите не понимаю решите пж
Приложения:
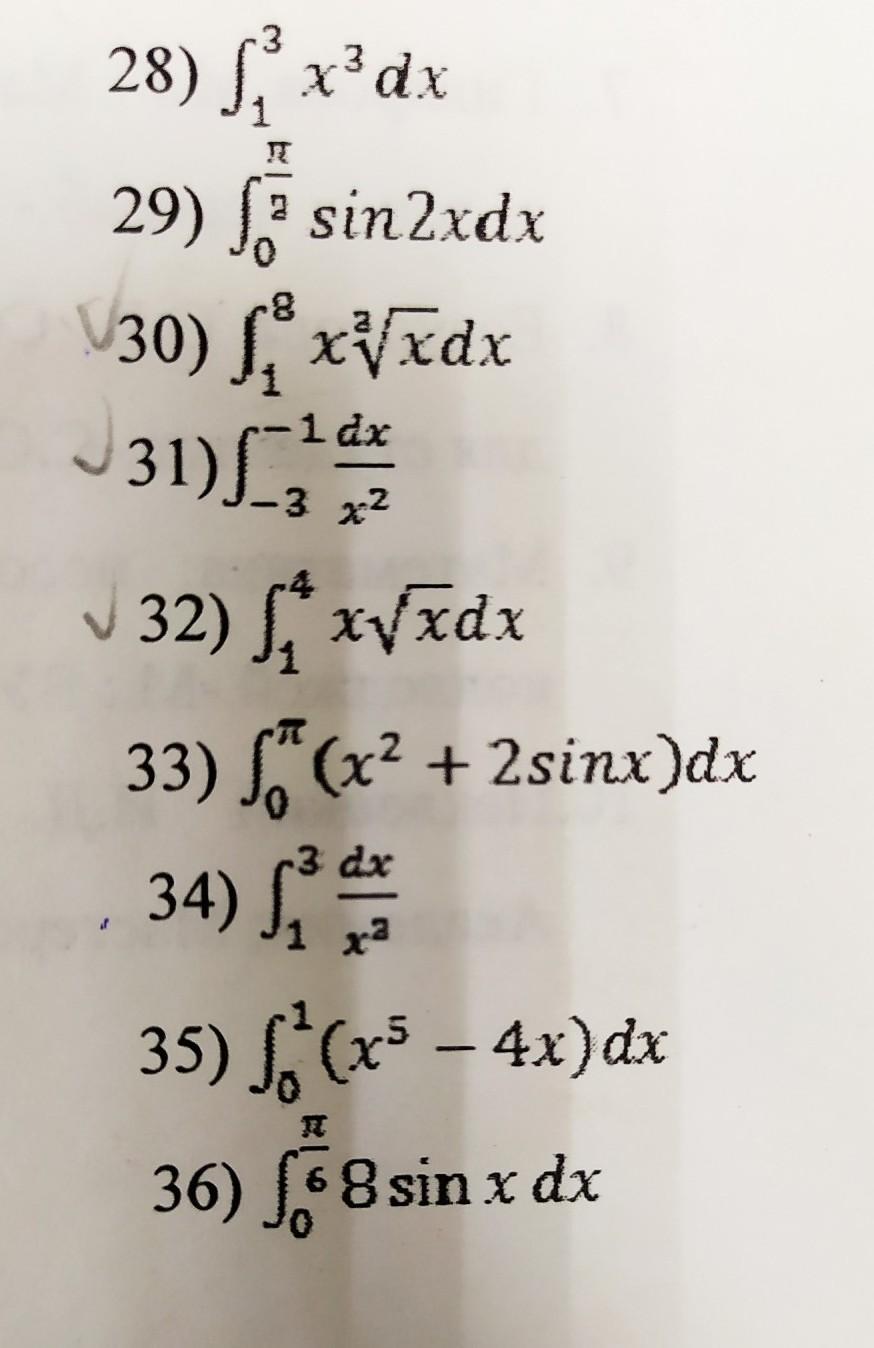
iknowthatyoufeelbro:
Только отмеченные?
да
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Алгебра,
автор: elizavetasilukova200
Предмет: Математика,
автор: ovbvblvlv
Предмет: Математика,
автор: daniilrudometov21
Предмет: Математика,
автор: nastenka110
Предмет: Химия,
автор: kuzenko01