Предмет: Алгебра,
автор: SheldonCooper12
хей всем
найти касательную
Приложения:
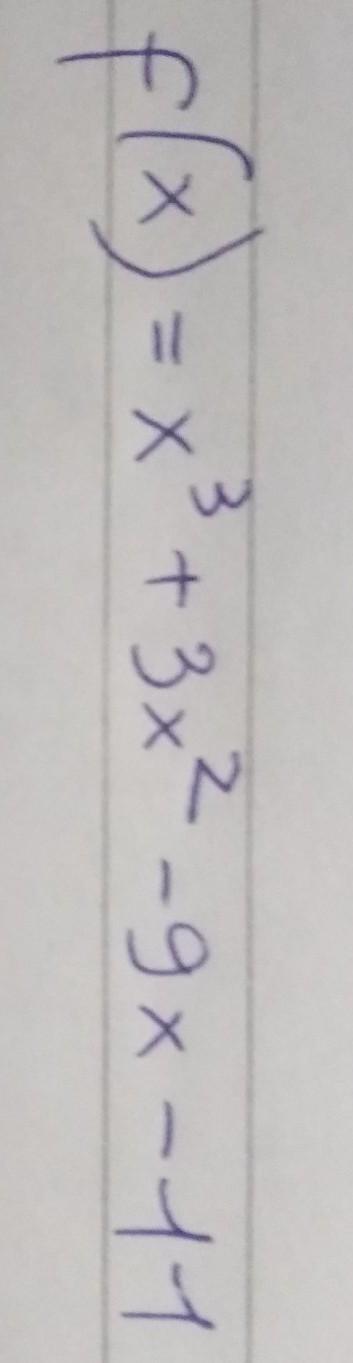
Аноним:
а в какой точке?
Ответы
Автор ответа:
1
Берем производную: f'=3x^2+6x-9
Приравниваем к нулю функцию: 3x^2+6x-9=0 <=> x^2+2x-3=0
Находим х: x1=-3 или x2=1
Находим что точка минимума, а что максимума (подставляем промежуточные значения в производную и смотрим на знак- с плюса на минус-max, наоборот-min): max=-3, min=1.
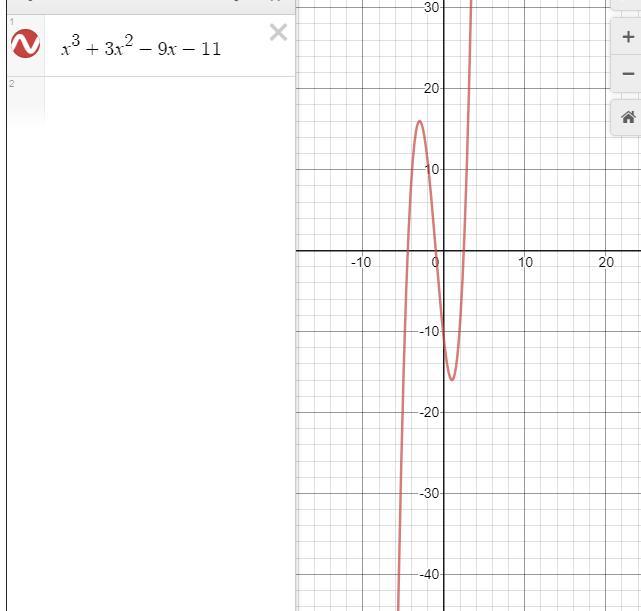
Понятно что касательная проходит по одной из точек экстремума(min, max).
Возьмем минимум (считать проще) и подставляем в функцию: f(1)=-16
y(игрик) найден и он равен -16
Т.к. вы попросили найти одну касательную, то подставить -3 в функцию ваша часть работы
Приложения:
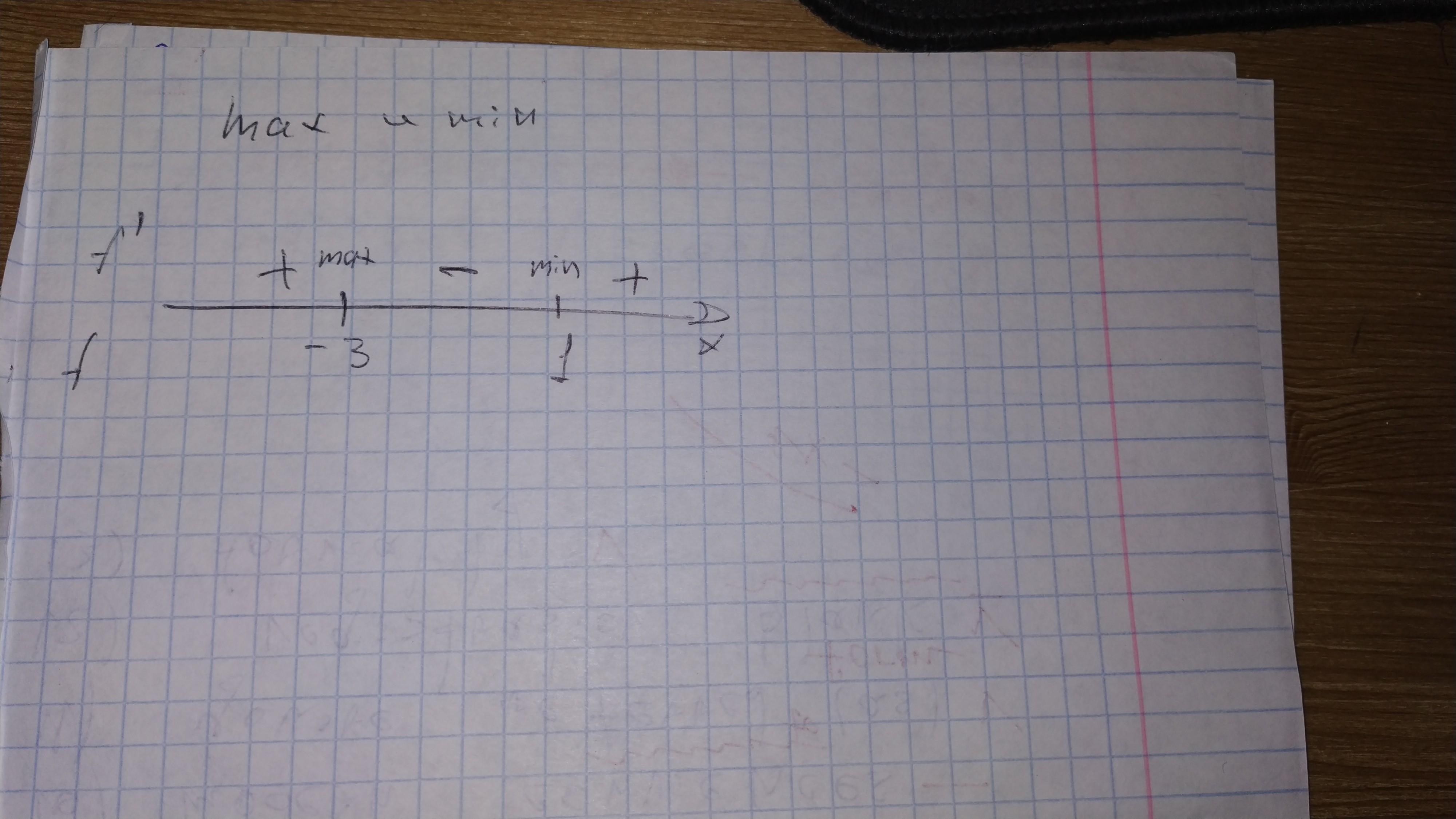
а как мы получили 3x^2+6x-9?
и как превратили в x^2+2x-3
3x^2+6x-9 - мы взяли производную от функции. можно посмтореть таблицу производных, если не понятно как именно.
x^2+2x-3
разделили на 3 предыдущее уравнение
разделили на 3 предыдущее уравнение
а вот ты решил дискриминат и получил корни и что дальше?
непонятно
я строю прямую. на ней отмечаю точки -3 и 1. подставляю значения между ними в производную, а также между -∞ и -3, между 1 и ∞. Если отрицательное число, то ставлю минус. Если положительное, то плюс.
Если первая производная идет с плюса на минус, то точка является точкой максимума функции. Если с минуса на плюс, то точкой минимума
вообще исходя из геометрического смысла производной, то понятно, что она равна углу наклона между касательной к графику и абциссой. а все действия, что я произвел нужны, чтобы через производную найти точку, где будет проходить касательная
Похожие вопросы
Предмет: Українська мова,
автор: kruganovskay1180
Предмет: Математика,
автор: no149151
Предмет: Английский язык,
автор: anastasiadik05
Предмет: Литература,
автор: artemgurdyale
Предмет: Математика,
автор: wan22211