Предмет: Алгебра,
автор: daniel23548
39 баллов
Найти область определения функции
1)

2)
![y = \sqrt[12]{5 - x} y = \sqrt[12]{5 - x}](https://tex.z-dn.net/?f=y+%3D+%5Csqrt%5B12%5D%7B5+-+x%7D+)
3)
![y = \frac{1}{ \sqrt[4]{x {}^{2} } - 11x + 10} y = \frac{1}{ \sqrt[4]{x {}^{2} } - 11x + 10}](https://tex.z-dn.net/?f=y+%3D+%5Cfrac%7B1%7D%7B+%5Csqrt%5B4%5D%7Bx+%7B%7D%5E%7B2%7D+%7D+-+11x+%2B+10%7D+)
Ответы
Автор ответа:
1
Решение приложено...
Приложения:
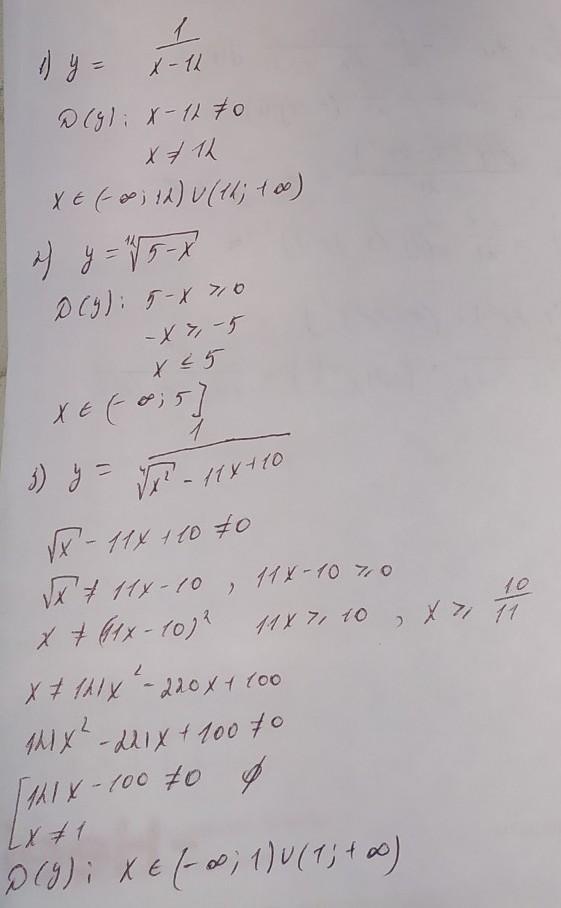
daniel23548:
Уважаю
Автор ответа:
1
Ограничение только на неравенство нулю знаменателя:
У нас корень четной степени, а значит, ограничением является неотрицательность подкоренного выражения:
По поводу 3-его у меня сомнения в правильности записи условия:
если условие такое, как записано, то есть
, то ограничение лишь на неравенство нулю знаменателя:
В данном случае получаем:
Рассматриваем 2 случая:
То есть
Но я сильно сомневаюсь, что там не все под корнем, рассмотрим этот случай:
Чтобы решить неравенство воспользуемся методом интервалов, нули уже нашли
и
, имеем +-+ на промежутках и
Похожие вопросы
Предмет: История,
автор: PsinaPsinovna
Предмет: Математика,
автор: amirazivotikova
Предмет: Алгебра,
автор: ostapenkavana228
Предмет: Литература,
автор: СУПЕРУМНЫЙУМНЯША
Предмет: Литература,
автор: olesyanelyubina