Предмет: Математика,
автор: vitalik2112
решите пожалуйста
найти производные y'x от следующих функций заданных в неявном виде
хоть что-то
Приложения:
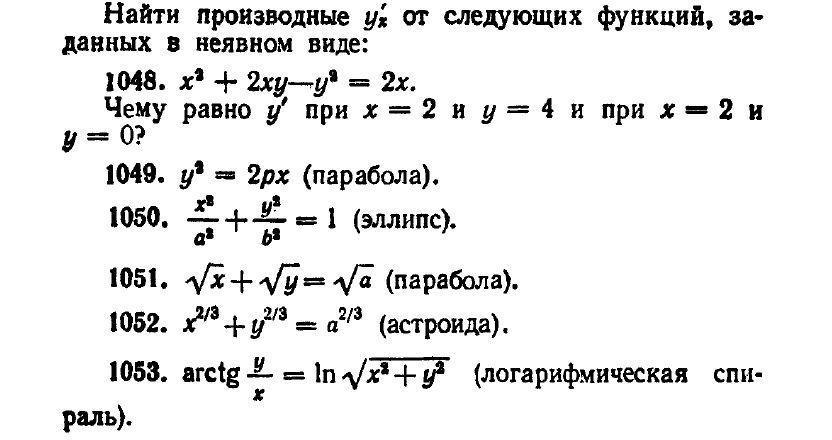
Ответы
Автор ответа:
2
То есть работаем как с обычными функциями и все правила дифференцирования работают. Только учитываем, что
vitalik2112:
Только в 1053 почему в ответе не y'=x+y/x-y?
Подправил) Я забыл в правой части взять внешнюю производную по логарифму, в итоге все гораздо проще получилось)
Похожие вопросы
Предмет: Химия,
автор: cepakelizaveta
Предмет: Биология,
автор: m19p
Предмет: Биология,
автор: arina76738
Предмет: Математика,
автор: Nastya070704
Предмет: Математика,
автор: DIDIDFA