Задание 2. Определить графически взаимное расположение линий. Если линии пересекаются, то указать точки пересечения. Определить вид линий.
x-2y-2=0 и x^2+y^2=4
Ответы
Пошаговое объяснение:
Определяем линии.
Это прямая линия и окружность радиусом R= √4 = 2
2*у = х-2 и у = 1/2*х - 1 - каноническая форму уравнения.
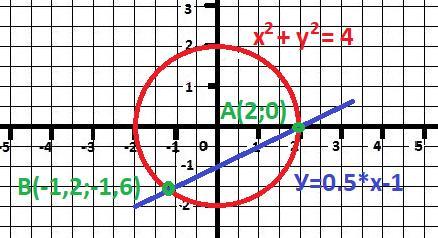
Рисунок к задаче в приложении.
Одна точка с явными координатами: А(2;0).
А для нахождения второй решим квадратное уравнение.
х = 2*y +2 - из уравнения прямой линии - подставим окружность.
(2*y +2)² + y² = 4
4*y² + 2*2*y*2 + 4 + y² = 4
5*y² + 8*y = 0 - квадратное уравнение - a*x² + b*x + c = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = 8² - 4*(3)*(0) = 64 - дискриминант. √D = 8.
Вычисляем корни уравнения.
у₁ = (-b+√D)/(2*a) = (-8+8)/(2*5) = 0/10 = 0 - первый корень
у₂ = (-b-√D)/(2*a) = (-8-8)/(2*5) = -16/10 = - 1,6 - второй корень
у1 = 0 и у2 = - 1,6 - координаты точек пересечения.
Вычисляем Х при У = - 1,6
х = 2*у + 2 = 2*(-1,6) + 2 = -1,2
В(-1,2;-1,6) - вторая точка пересечения - ответ.