Предмет: Математика,
автор: nastamaj78
решите матричное уравнение
Приложения:
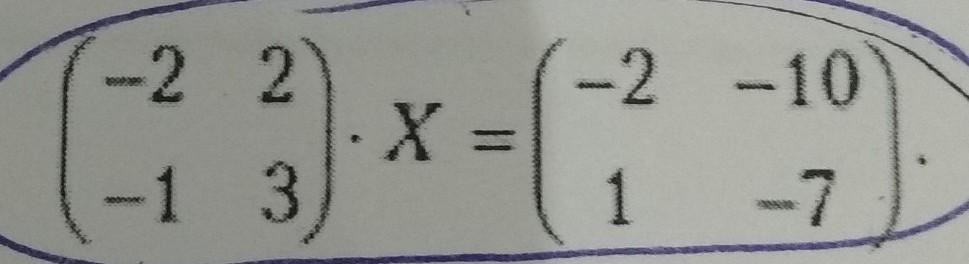
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Решением уравнения является
.
Найдем , где:
det(A) = -2*3 - (-1)*2=-4 - определитель матрицы A
- матрица из алгебраических дополнений
- присоединенная матрица для матрицы A
Похожие вопросы
Предмет: Физика,
автор: ramazanutarbaev6
Предмет: Математика,
автор: aleksejsmavgonec1
Предмет: Литература,
автор: davudko555
Предмет: Математика,
автор: патрик55555