Предмет: Алгебра,
автор: khkov99
Помогите срочно решить 35 балоа
Приложения:
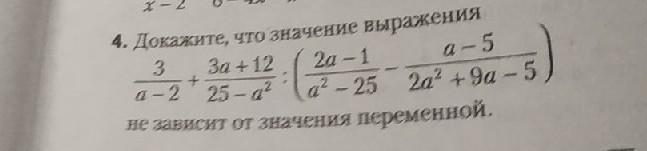
Ответы
Автор ответа:
0
Ответ:
Доказано.
Объяснение:
Пусть a=x:
Упростим выражение перед скобка
Упростим выражение в скобках:
Продолжим упрощение:
Завершим упрощение:
Итого получили, что выражение принимает значение -2 при любом значении переменной, а значит не зависит от неё.
Автор ответа:
0
Переменная сокращается, поэтому от нее значение выражения не зависит
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: dianochkase
Предмет: Алгебра,
автор: floppi62
Предмет: Математика,
автор: ilnariasakirova766
Предмет: Биология,
автор: firuza12v
Предмет: Литература,
автор: anastasiyasoko3