Предмет: Математика,
автор: Kristoforeska
Вокруг ривнобедренного треугольника MNP с основанием MP описано окружность с центром О. Найти углы треугольника, если угол PMO = 36 градусов. Сколько решений имеет задача?
Ответы
Автор ответа:
3
Ответ:
1-е решение: 63°, 63°, 54°; 2-е решение 27°, 27°, 126°
Пошаговое объяснение:
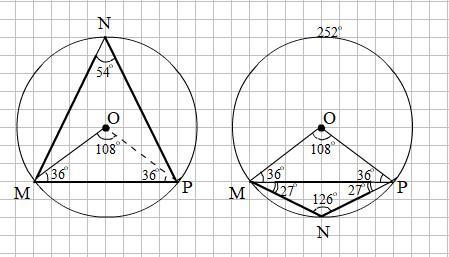
Задача имеет 2 решения. Смотри рисунок на прикреплённом фото.
Решение 1.
ΔMOP - равнобедренный, так как ОР = ОМ = R ⇒ ∠МРО = ∠РМО = 36°.
В ΔMOP угол при вершине О ∠МОР = 180° - 2·36° = 108°.
∠MNP = 108°/2 = 54° - как вписанный угол, опирающийся на дугу 180°
∠NMP = ∠ NPM = (180° - 54°)/2 = 63°.
Решение 2.
ΔMOP - равнобедренный, так как ОР = ОМ = R ⇒ ∠МРО = ∠РМО = 36°.
В ΔMOP угол при вершине О ∠МОР = 180° - 2·36° = 108°.
Дуга окружности ∪MNP = 108° ⇒ дуга ∪МР = 360° - 108° = 252°
Вписанный ∠MNP = 252°/2 = 126° как опирающийся на дугу МР.
∠NMP = ∠ NPM = (180° - 126°)/2 = 27°.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: login917649
Предмет: История,
автор: nastya264536
Предмет: Химия,
автор: dasksh8642
Предмет: Математика,
автор: Yerbro
Предмет: Математика,
автор: zari88