Предмет: Геометрия,
автор: noumchel
Уравнение окружности с определением центра и радиуса.
Напиши уравнение окружности, которая проходит через точку 4 на оси Ox и через точку 6 на оси Oy, если известно, что центр находится на оси Oy.
(Рассчитай в дробях и дроби запиши несокращёнными.)
Приложения:
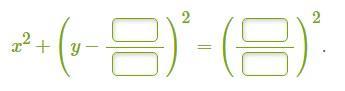
Ответы
Автор ответа:
0
Уравнение окружности (х-хо)²+(у-уо)²=R²
точка (хо; уо) - центр окружности. По условию хо=0. х²+(у-уо)²=R²
На ней лежат точки (4; 0) и (0; 6)
У всех точек на оси ОХ у=0
У всех точек на оси ОУ х=0
Подставим координаты точек в уравнение окружности.
{16+(0-уо)²=R²
{0+(6-yo)²=R²
{16+yo²=R²
{ 36-12yo+yo²=R² вычтем
16-36+12уо=0
12уо=20; уо=20/12=5/3 центр окружности (0; 5/3)
х²+(у-5/3)²=R² подставим в уравнение точку (4;0)
16+25/9=R²; R²=16*9/9 + 25/9=(144+25)/9=169/9=(13/3)²; R=13/3
Ответ: х²+(у-5/3)²=(13/3)².
Похожие вопросы
Предмет: Биология,
автор: sh1mo
Предмет: Русский язык,
автор: hsjdfnfdjahfn
Предмет: Физика,
автор: alinachka855
Предмет: Математика,
автор: guselnikova1
Предмет: Математика,
автор: ДноКрая