Предмет: Алгебра,
автор: ЛеммингЛеня
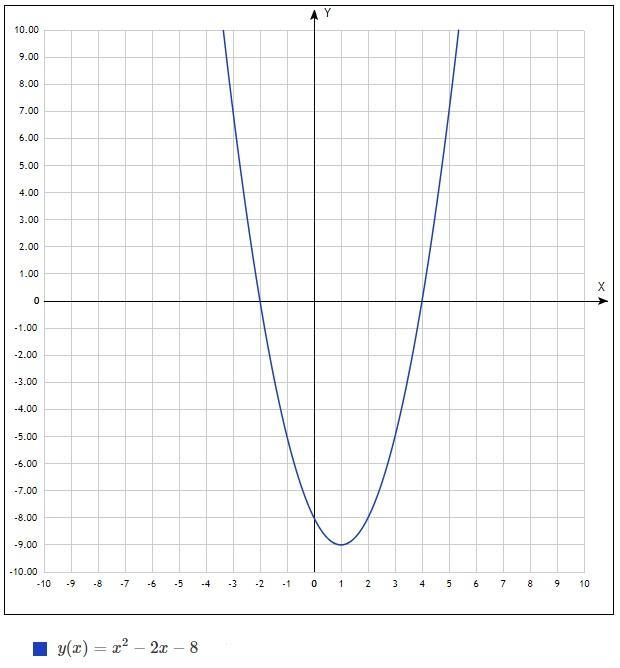
Постройте график функции  и найдите, пользуясь графиком
и найдите, пользуясь графиком
1. значения у, при которых х=3;-1,5
2. значения х, при которых у=-5;2
3. точки пересечения графика с осями координат
Ответы
Автор ответа:
1
Это квадратичная функция, график - парабола, получается путем перенесения по ОХ на 1 ед вправо и на 9 ед вниз по ОУ.
Можно и вычислить, а потом по графику посмотреть
1.
2.
То есть в первом случае для одного Y нашлось 2 значения Х, во втором случае - ни одного.
Вообще странно, всё это по графику нормально не посмотришь.
3. Точки пересечения:
с осью ОУ при
с осью ОХ при
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Semen9009
Предмет: Українська мова,
автор: ishmyheliyk
Предмет: Математика,
автор: lebeddinka666
Предмет: История,
автор: Diana18111
Предмет: География,
автор: IVAN546847