Question

докажите что через любую точку прастранства не лежащую на даной прямой Проходит прямая параллельная данной и притом только одна ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО НУЖНО​

Answer 1

Пошаговое объяснение:

1) Докажем существование прямой.

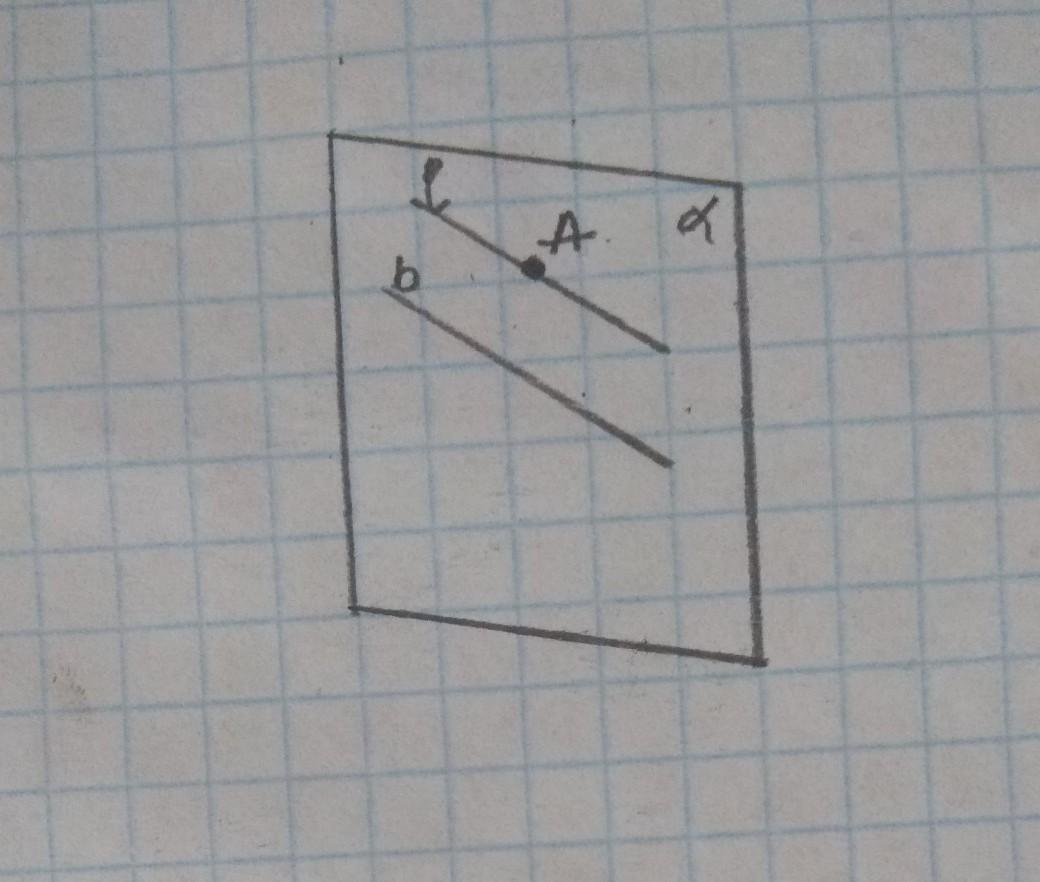
Пусть дана прямая b и точка А, не лежащая на этой прямой. Тогда через них проходит единственная плоскость a(см. рисунок). В этой плоскости, как известно из планиметрии, существует прямая l, проходящая через точку А и параллельная прямой b.

2. Докажем единственность прямой.

Предположим, что существует ещё одна прямая l1, проходящая через точку А и параллельная прямой b. Тогда прямая l1 должна лежать в одной плоскости с точкой А и прямой b, тоесть в плоскости а. Из курса планиметрии известно, что в плоскости а через точку А проходит единственная прямая, параллельная прямой b. Значит, прямая l1 совпадает с прямой l.

Теорема доказана

Answer 2

Дано:

точка M; M не лежит на прямой a;


Доказательство:

1) Через прямую a и точку M проходит плоскость α, и притом только одна (по аксиоме стереометрии).

2) Прямая, параллельная прямой a и проходящая через M должна лежать в одной плоскости с прямой a, то есть в α. Но в плоскости α (по теореме планиметрии) через точку M проходит прямая, параллельная данной, и притом только одна.

Что и требовалось доказать.