Question

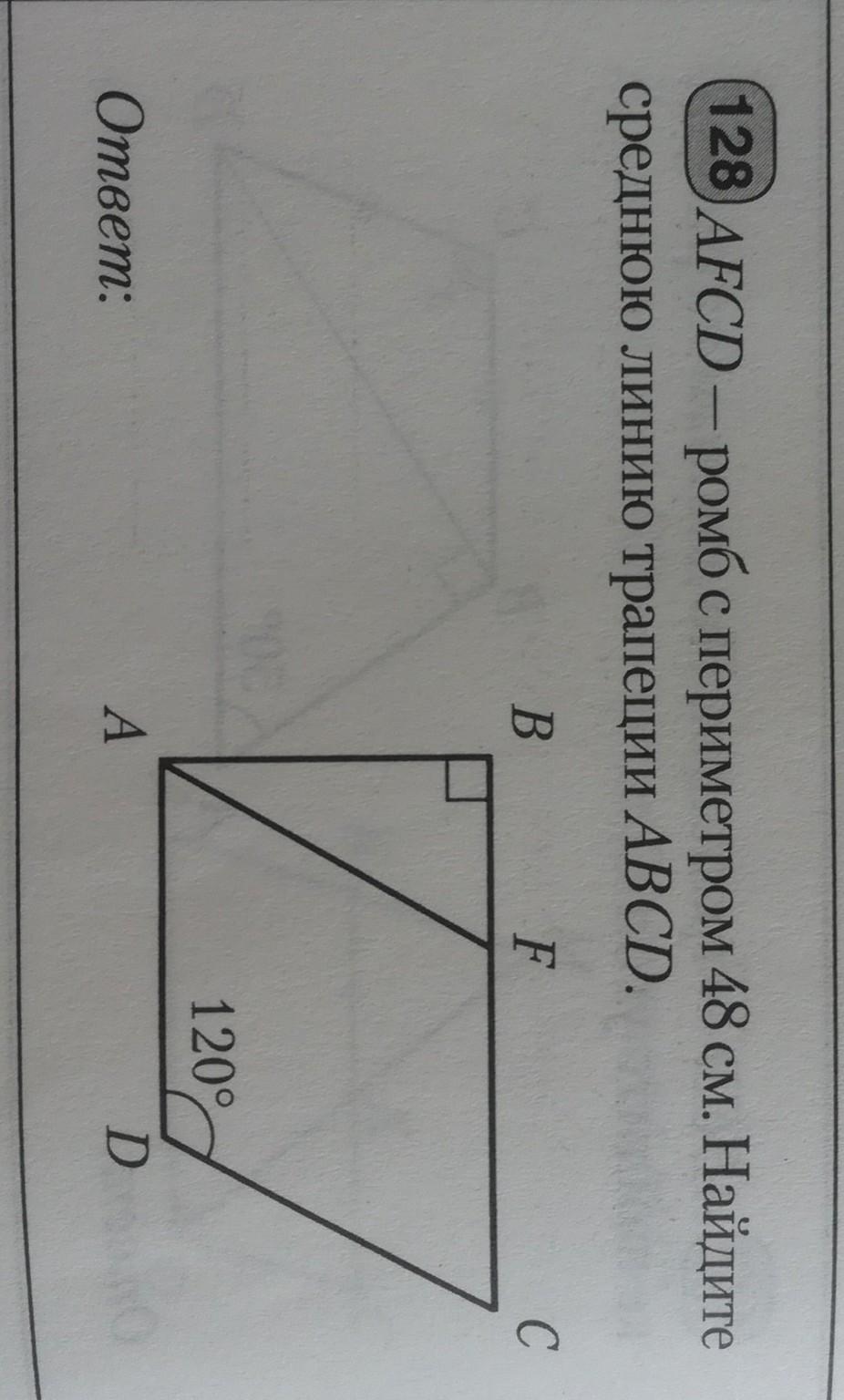
Помогите пожалуйста решить​

Answer 1

Ответ:

15 см

Объяснение:

Рассмотрим ромб AFCD. В нем ∠D=∠F=120°. Значит

∠A=∠C=(360-(120+120))÷2=60° (т.к. сумма внутренних углов четырёхугольника равна 360 градусов).

Сделаем дополнительное построение: проведем диагональ DF. Получили 2 равных равносторонних ΔAFD=ΔCDF, т.к. диагональ DF образовала 4 угла по 120÷2=60°.

Значит все стороны ромба равны и длина каждой из них равна 1/4 периметра, т.е. 48÷4=12 см.

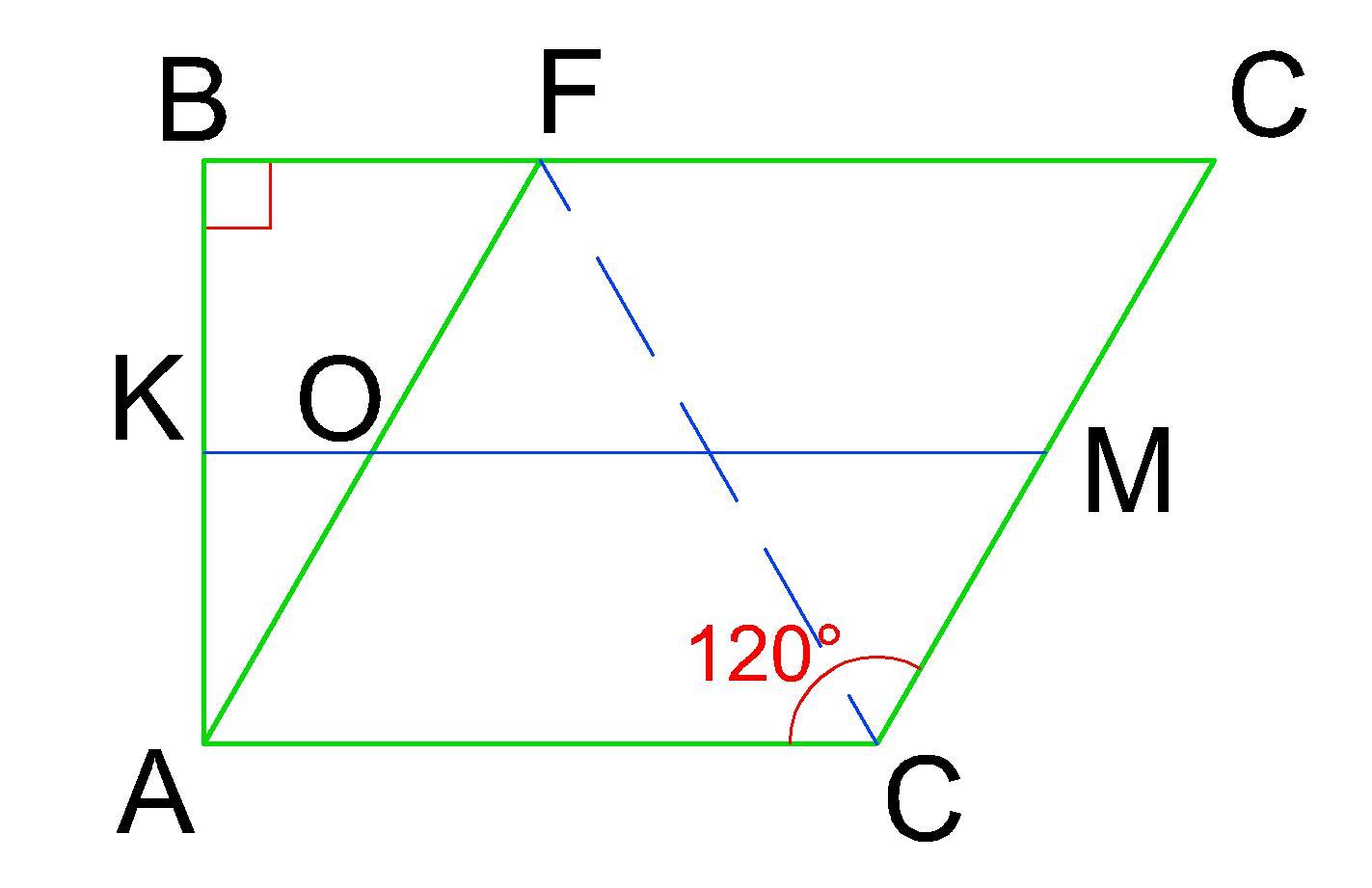
Проведём среднюю линию KM трапеции ABCD. Пусть КМ пересекает сторону AF в точке О. Тогда КМ=КО+ОМ.

Очевидно, что ОМ равна стороне ромба.  ОМ=12 см.

Найдём КО из прямоугольного ΔКОА.

∠ОАК=∠DAB-∠DAF=90-60=30°

Гипотенуза АО равна половине стороны AF (т.к. образована средней линией). АО=12÷2=6 см.

Катет КО=АО·sin∠ОАК=6·sin30°=3 см.

Значит КМ=12+3=15 см