Предмет: Математика,
автор: mahmudova140467
плиииз я столько пыталась,не выходит
Приложения:
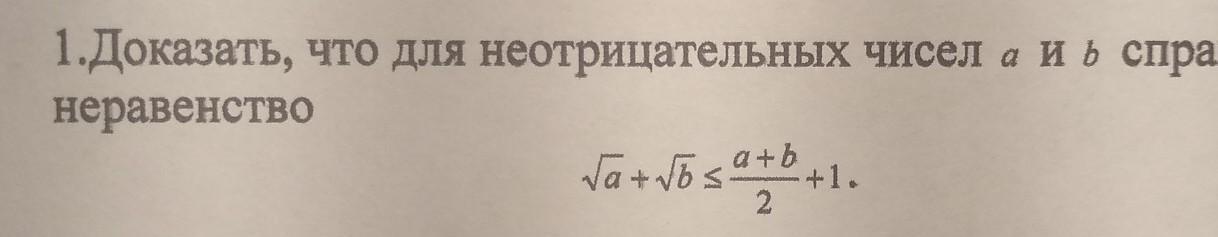
Ответы
Автор ответа:
2
Ответ:
Доказательство в объяснении
Пошаговое объяснение:
Рассмотрим разность
Тогда
или
Что требовалось доказать.
Похожие вопросы
Предмет: Геометрия,
автор: nastymi33
Предмет: Литература,
автор: ivanovbagren
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: kirillknotko15kirill
Предмет: Литература,
автор: Карина5666