Предмет: Алгебра,
автор: kingpineapple
Помогите решить пожалуйста
Приложения:
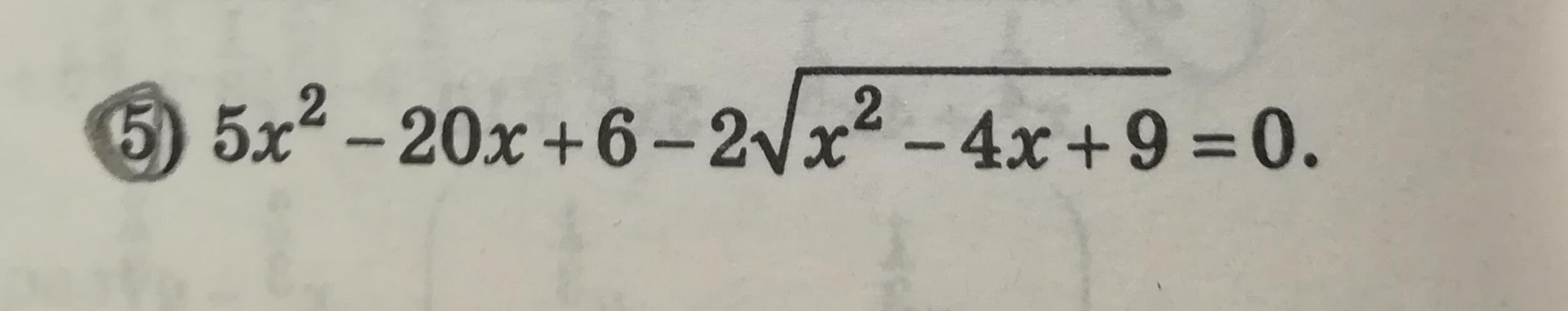
Ответы
Автор ответа:
1
ОДЗ
при любых x. Координаты вершины параболы (x,y)=(2,5), ветви направлены вверх.
Распишем уравнение
Обозначим
Корней нет.
Ответ: x=0 и x=4.
Universalka:
В последнем уравнении D>0 и имеем еще два корня (-10 +2*корень из 11)/5 и (-10 - 2*корень из 11)/5.
Похожие вопросы
Предмет: Биология,
автор: vitalikmakeev62
Предмет: Алгебра,
автор: MaxArtick
Предмет: Химия,
автор: zvoz
Предмет: Математика,
автор: Murad11111fhtfdf