Предмет: Алгебра,
автор: TalismDascha
Даю 100 баллов, помогите найти неопределённые интегралы методом подстановки
Приложения:
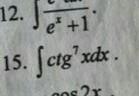
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Физика,
автор: sony34970
Предмет: Литература,
автор: 1melmary2010
Предмет: Химия,
автор: belikovaulia95
Предмет: Химия,
автор: serega12488