Предмет: Алгебра,
автор: TalismDascha
Даю 50 баллов.
Найдите интеграл методом подстановки
Приложения:
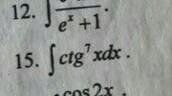
ВикаБач:
y=sinx ???
Ответы
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Спасибо большон
ошибка в знаке при делнии
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: asobu
Предмет: Алгебра,
автор: phoneberezne13
Предмет: Математика,
автор: varavkina
Предмет: Математика,
автор: asasin85
Предмет: Математика,
автор: kyktepta640