Question

Найдите площадь фигуры...

Answer 1

Ответ:

Объяснение:

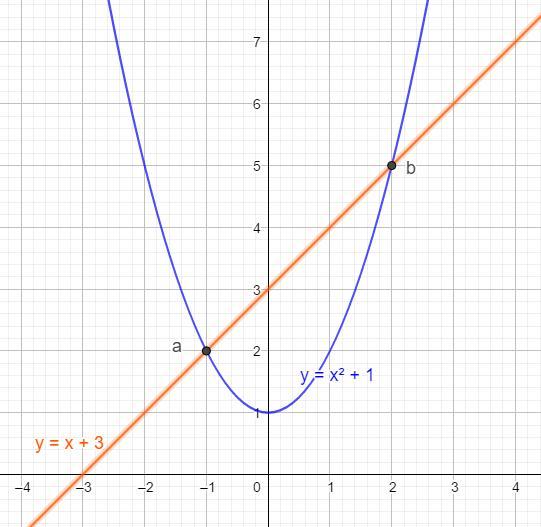
Найдем точки пересечения параболы y = x² + 1 и прямой y = x + 3

$\[\left\{\begin{gathered}y={x^2}+1\hfill\\y=x+3\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}{x^2}+1=x+3\hfill\\y=x+3\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}{x^2}-x=2\hfill\\y=x+3\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}{x^2}-x-2=0\hfill\\y=x+3\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}{x_1}=-1,{x_2}=2\hfill\\{y_1}=2,{y_2}=5\hfill\\\end{gathered}\right.\]$

Парабола и прямая пересекаются в точках (-1; 2) и (2; 5)

Для того, чтобы получить площадь фигуры ограниченной линиями, необходимо вычислить определенный интеграл вида:

$\displaystyle \[\int\limits_a^b{\left({f(x)-g(x)}\right)}dx\]$

где a = x₁; b = x₂

$\displaystyle \[\int\limits_{-1}^2{(x+3)dx-\int\limits_{-1}^2{({x^2}+1)dx=}}\left({\frac{{{x^2}}}{2}+3x}\right)\mathop|\limits_{-1}^2-\left({\frac{{{x^3}}}{3}+x}\right)\mathop|\limits_{-1}^2=\]$

$\displaystyle\[\left({\left({\frac{{{2^2}}}{2}+3\cdot2}\right)-\left({\frac{{-{1^2}}}{2}+3\cdot(-1)}\right)}\right)-\left({\left({\frac{{{2^3}}}{3}+2}\right)-\left({\frac{{-{1^3}}}{3}+(-1)}\right)}\right)=\left({8+2.5}\right)-\left({\frac{{14}}{3}+\frac{4}{3}}\right)=10.5-6=\boxed{4.5}\]$