Question

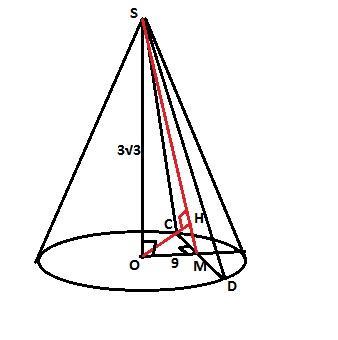
В основі конуса проведено хорду CD на відстані 9см від центра О. СО висота =3 корня из 3 см.
Знайти відстань від точки О до площини CSD.

Answer 1

Ответ:

ОН = 3√3·9/(6√3) = 4,5 см.

Объяснение:

Проведем радиус основания, перпендикулярно хорде CD и на пересечении с хордой отметим точку М. Тогда в прямоугольном треугольнике SOM катет ОМ = 9см, катет SO = 3√3 см, а гипотенуза SM по Пифагору равна √108 = 6√3 см.

В прямоугольном треугольнике OSM высота ОН - искомое расстояние, так как ОН перпендикулярна SM, а плоскость ОСМ перпендикулярна плоскости CSD.

ОН - высота из прямого угла треугольника и по формуле равна:

ОН = 3√3·9/(6√3) = 4,5 см.