Question

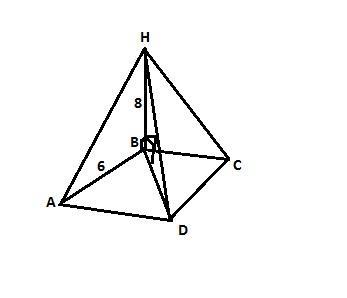
через вершину B квадрата ABCD проведена прямая BH ,перпендекулярна я её плоскости . найдите расстояние от трчки H до прямых, содержащих стороны квадрата, если BH=8 см, а AB=6 см. Помогите пожалуйста с решением и чертежом.

Answer 1

Ответ:

ВН = 8см, АН = СН = 10см, DH = 2√34 см.

Объяснение:

ВН перпендикулярна плоскости АВСD, значит треугольники АВН, СВН и DBH прямоугольные. В этих треугольниках катет ВН общий, катет АВ = ВС = 6см (стороны квадрата), катет

BD = 6√2 (диагональ квадрата). Искомые расстояния - гипотенузы АН и СН и DH. Четвертое расстояние - перпендикуляр ВН нам дан.

Тогда по Пифагору:

АН = СН = √(8²+6²) = 10 см.

DH = √(8²+BD²) = √(64+72) = √136 = 2√34 см.