Question

В параллелограмме АВСД, проведена биссектриса АК, которая делит сторону ВС на отрезки 4 и 6. Найдите периметр параллелограмма и среднюю линию трапеции АКСД
ПОМОГИТЕ

Answer 1

Ответ:

28 см;  8 см.

Объяснение:

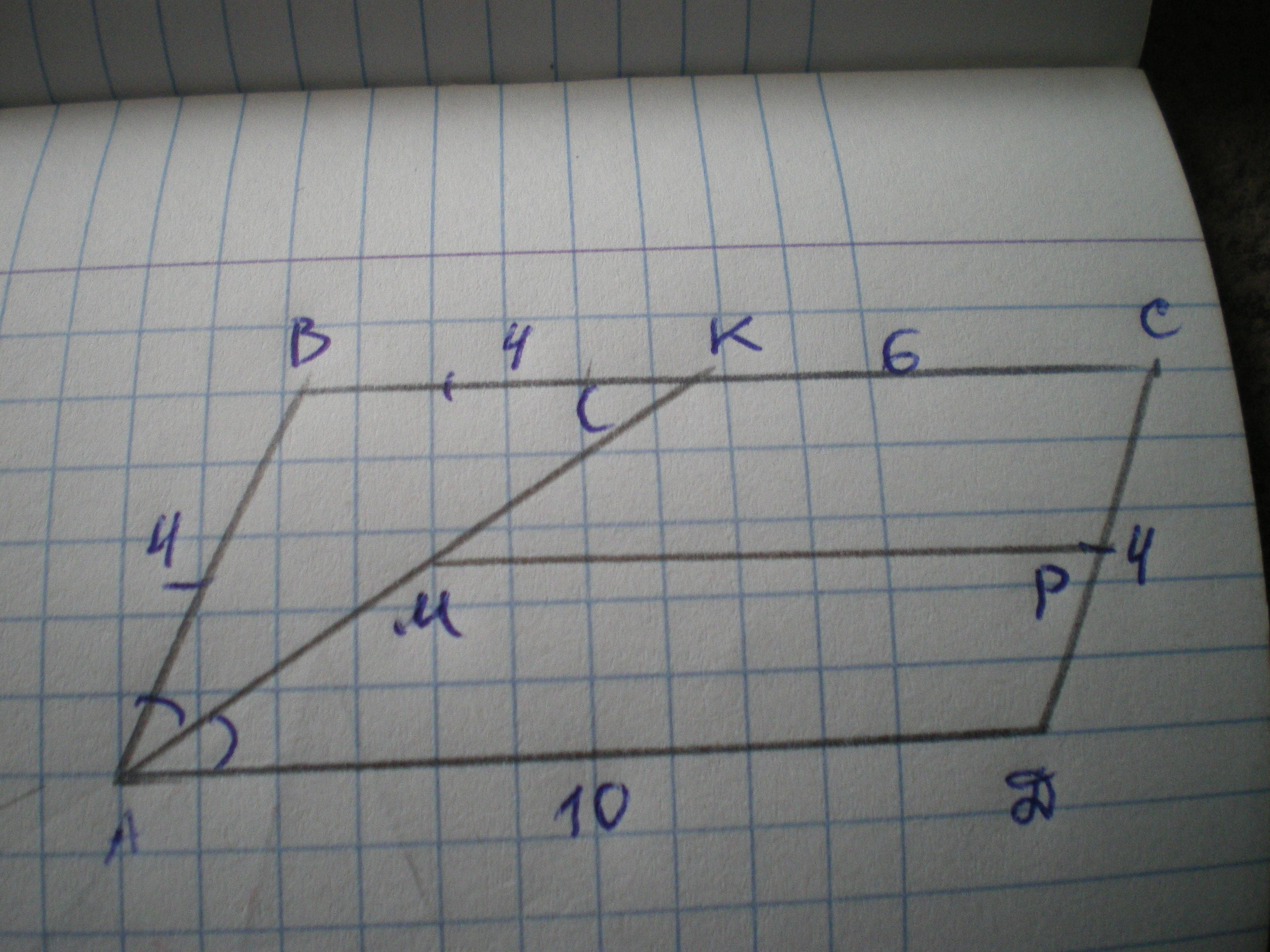
Дано: АВСD - параллелограмм, АК - биссектриса, ВК=4 см, КС=6 см. Найти Р (АВСD), среднюю линию АКСD.

Рассмотрим ΔАВК - равнобедренный (∠ВАК=∠КАD по определению биссектрисы, ∠ВКА=∠КАD  как внутренние накрест лежащие при ВС║АD и секущей АК), значит АВ=ВК=4 см.

АD=ВС=6+4=10 см;  СD=АВ=4 см (как противоположные стороны параллелограмма)

Р=10*2+4*2=28 см.

МР - средняя линия АКСD (трапеции)

МР=(АD+КС)/2=(6+10):2=8 см