Предмет: Математика,
автор: angryhan
Помогите пожалуйста!!!!! СРОЧНО!!!!!
Приложения:

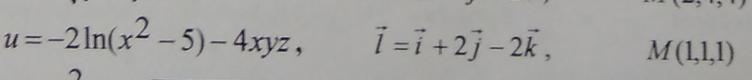
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: lany67444
Предмет: Алгебра,
автор: maryanatyan2016
Предмет: Геометрия,
автор: russkihmariya05
Предмет: Математика,
автор: ermilovlexa2012