Предмет: Алгебра,
автор: LeraBat18
Помогите решить производные
f(x)=(2/x)-(8/√x)+(6/3√x^2)+2x+6x^2√x
Остальное не фото
Буду очень благодарна!
Приложения:
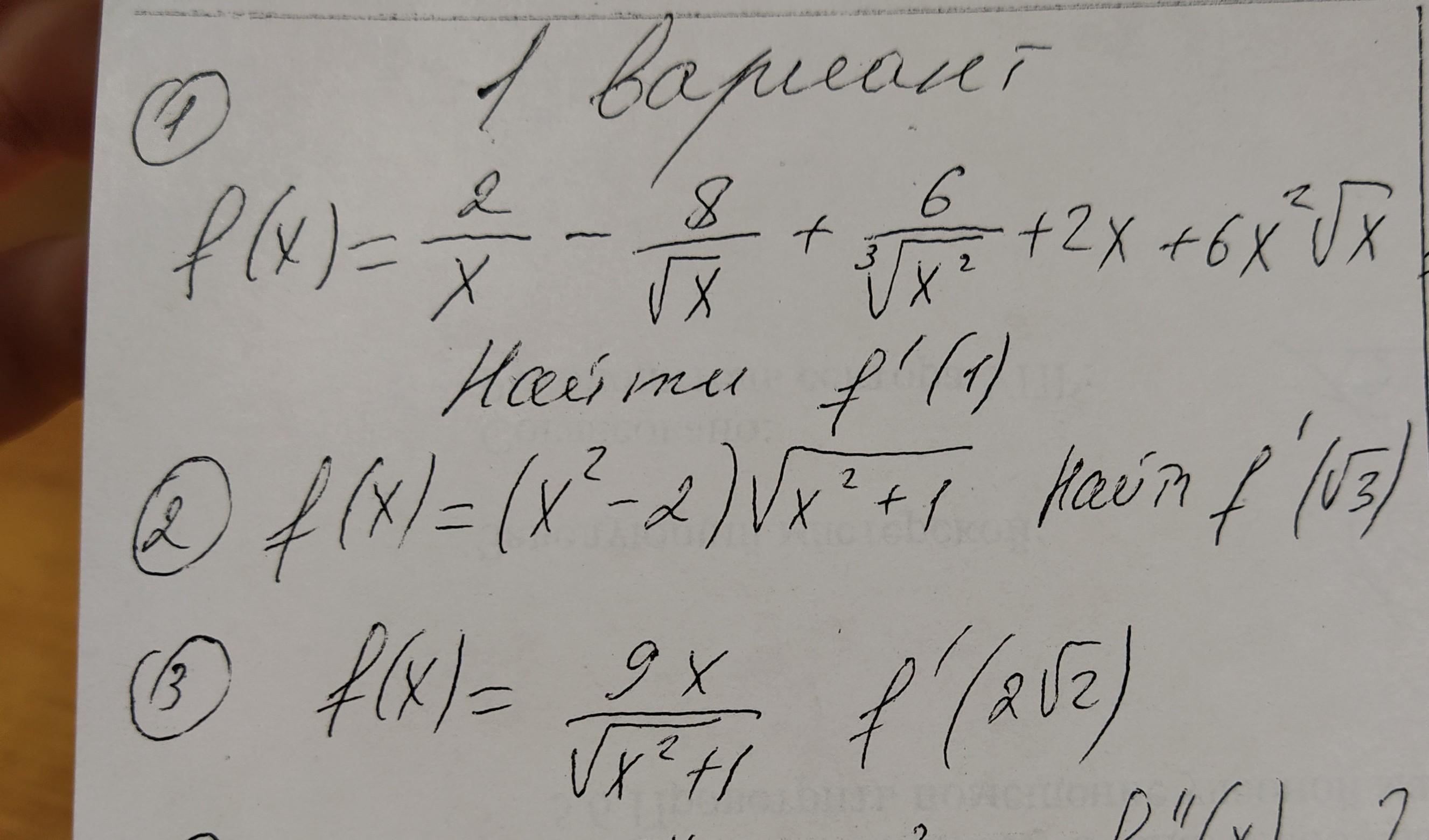
Ответы
Автор ответа:
6
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Математика,
автор: polinakurocka955
Предмет: Математика,
автор: budarina2010
Предмет: Другие предметы,
автор: mikola18
Предмет: Математика,
автор: NIPash