Предмет: Математика,
автор: ARproVL
ДАЮ 50 БАЛЛОВ. ПОМОГИТЕ С РЕШЕНИЕМ
Приложения:
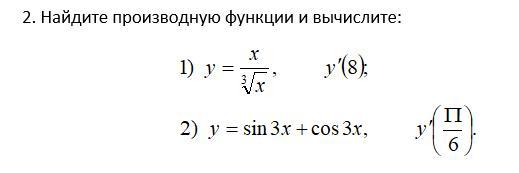
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: История,
автор: andreykorobov10
Предмет: Физика,
автор: polina09055
Предмет: История,
автор: zaychikvlad
Предмет: История,
автор: GanBeat
Предмет: Обществознание,
автор: Ava1212