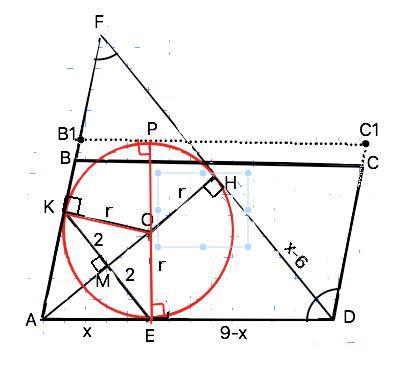
Биссектриса угла D параллелограмма ABCD пересекает продолжение стороны AB в точке F. Окружность, вписанная в треугольник ADF , касается стороны AD в точке E , а отрезка AB в точке K.
а) Найти радиус окружности, если AD=9, KE=4 и AE меньше ЕD.
б) При дополнительном условии, что окружность касается стороны BC параллелограмма, найти площадь параллелограмма.
Ответы
Ответ: а) 6/√5 (ед. длины). б) 108/√5=21,6√5 (ед. площади)
Объяснение: Центр окружности, вписанной в треугольник, лежит на биссектрисе его угла.⇒ АН - биссектриса угла ВАD, О - центр окружности. ОК и ОЕ - радиусы, проведенные к точкам касания. По свойству отрезков касательных, проведенных к окружности из одной точки. АК=АЕ; DE=DH; FK=FH
Примем АК=АЕ равным х. Тогда ЕD=DH=9-х.
а) Рассмотрим рисунок приложения. Угол AFD=∠CDF (накрестлежащие при FA||CD и секущей FD) Но ∠CDF=∠ADF (DF- биссектриса ) ⇒ ∠АFD=∠FDA. ⇒ ∆ FAD – равнобедренный и AF=AD=9.
АН - биссектриса угла равнобедренного треугольника, ⇒ АН – его высота и медиана ( свойство). ⇒ FН=НD=9-х
Аналогично в ∆ КАЕ биссектриса АМ равнобедренного ∆ АКЕ - медиана и высота. ⇒ КМ=МК=4:2=2.
Прямоугольные ⊿ МАЕ и ⊿ НAD подобны по общему острому углу при А. Из подобия следует отношение DH:ЕМ=DA:ЕА.
т.е. (9-х):2=9:х., откуда получаем х²-9х+18=0. По т.Виета х₁+х₂=-(-9)=9; х₁•х₂=18 ⇒ х₁=3; х₂=6
По условию АЕ< AD, поэтому АЕ=3, ED=6
Из ⊿ АНD по т.Пифагора АН=√(AD*-DH*)=√(81-36)=3√5
⊿ АОЕ и ⊿ АDH подобны по общему углу при вершине А, из чего следует ОЕ:DH=AE:AH ⇒ r=AE•DH:AH =3•6:3√5.=6/√5.
б) При условии, что окружность касается стороны BC параллелограмма, диаметр РЕ окружности, вписанной в угол ВАD, будет высотой параллелограмма. S=h•a=2r•AD=(12/√5)•9=108/√5. = 21,6√5 (ед. площади)