Предмет: Геометрия, автор: misternabiulli

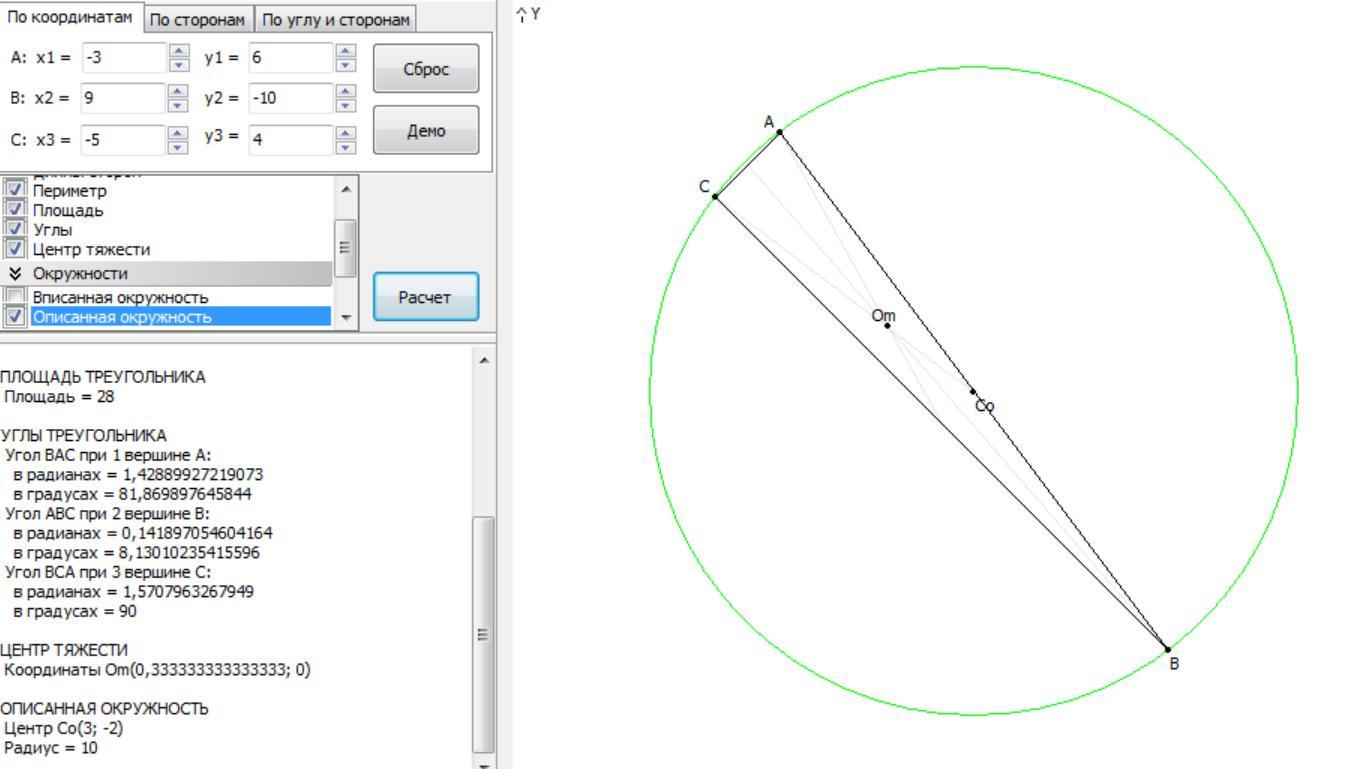
Даны вершины треугольника А (-3; 6) В (9; -10) С (-5; 4).
Найдите координаты центра и радиус описанного около него круга.

Ответы

Автор ответа: dnepr1
2

Даны вершины треугольника А (-3; 6) В (9; -10) С (-5; 4).

Определим длины сторон.

АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √400 =  20.

BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √392 ≈ 19,799.

AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √8 ≈ 2,828.

Как видим, треугольник прямоугольный (сумма квадратов двух сторон равна квадрату третьей).

Координаты центра О  описанного около него круга находим как середину гипотенузы АВ.

О((-3+9)/2=3; (6-10)/2=-2) = (3; -2).

Радиус равен половине гипотенузы: R = 20/2 = 10.

Приложения:
Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Биология, автор: mary8715
Позначте рослину, в якої розвиваються весняні спороносні і літні

фотосинтезуючі пагони:

1.щитник чоловічий

2.плаун булавовидний

3.зозулин льон.

4.хвощ польовий
5 лет назад
Предмет: История, автор: ItsMyNickname
Фрагмент какой картины? (Эпоха Возрождения)
5 лет назад
Предмет: Информатика, автор: sofeykaaa4

Помогите пожалуйста очень срочно !!!

Завдання 1-14 по 0,5 бала
1. Яка команда підключає модуль графічного вікна:
а) from math import*
б) from turtle import*
в) from tkinter import*
г) from tkinter.messagebox import*
2. Якій конструктор(команда) сторює графічне вікно?
а) tkinter
б) Tk
в) Lebel
г) title
3. Якою командою задаються розміри вікна?
а) Window.geometry()
б) Window.title()
в) Window.place
4. За допомогою якого конструктора можна додати напис?
а) Tk()
б) Button()
в) Label()
г) Entry()
5. Для розташування елемента керування у вікні використовується метод ...
а) pack()
б) title()
в) geometry()
г) bind()
6. Для розташування у графічному вікні тестового поля використовується такі команди:
а) змінна=entry()
змінна.pack()
б) змінна=Label()
переміна.pack()
в) змінна=Entry()
змінна.pack()
г) змінна=Button()
змінна.pack()
7. Яка команда (службове слово) що вказує на створення функції
а) def
б) place
в) Button
г) get
8. Для отримання значення, яке містить текстове поле використовується метод а) get()
б) place()
в) title()
9. Для виведення вікна повідомлення використовується модуль
а) from math import*
б) from turtle import*
в) from tkinter.messagebox import*
г) from tkinter import*
10. Перимикачі створюють за допомогою конструктора …
а) Lebel
б) Radiobuttton
в) tkinter
г) Entry
11. Для створення прапорця використовують команду …
а) Checkbutton
б) Entry
в) Tk
г) tkinter
14 Синтаксис умовного циклу має такий вигляд:
а) while умова:
команда
б) while умова
команда:
в) for i in range(n)
команда
г) for i in range(n):
команда
13. Синтаксис циклу з лічильником має такий вигляд:
а) while умова:
команда
б) while умова
команда:
в) for i in range(n):
команда
г) for i in range(n)
команда:
14. for i in range(2,10,2) виведе числа
а) 2 4 6 8 10
б) 2 4 6 8
в) 0 2 4 6 8 10
г) 2 3 4 5 6 7 8 9 10
15. (2 бали) Виконайте фрагмент програми та з’ясуйте, якими будуть значення змінних після його завершення:
16. (3 бали) Створіть проєкт для обчислення середнього арифметичного додатних чисел, перше з яких дорівнює 100, а кожне наступне менше від попереднього на задане додатне число.
5 лет назад
Предмет: История, автор: сереня777
Какие признаки свидетельствуют о развитии капитализма в России в XIX в.?
8 лет назад
Предмет: Геометрия, автор: Ромео227
Дано: C(-4;4); D(6;1). составим уравнение окружности. ребят, пж
8 лет назад