Предмет: Геометрия,
автор: hokkhokk
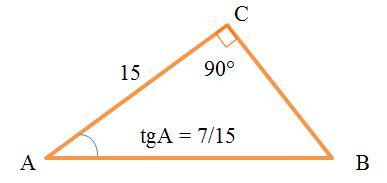
В треугольнике АВС угол С равен 90 градусов, АС = 15, tgA = 7/15. Найдите BC. Подробное решение, пожалуйста.
Ответы
Автор ответа:
13
Ответ:
7 (единиц)
Объяснение:
Дано:
В ΔABC (см. рисунок)
∠C=90°
АС = 15
tgA = 7/15
Найти: BC.
Решение. В прямоугольном треугольнике с катетами AC, BC и гипотенузой AB, тангенс угла A определяется по формуле:
tgA = BC/AC.
Отсюда, в силу АС = 15 и tgA = 7/15:
BC= tgA•AC= 7/15•15=7 (единиц).
Приложения:
Автор ответа:
5
Дано :
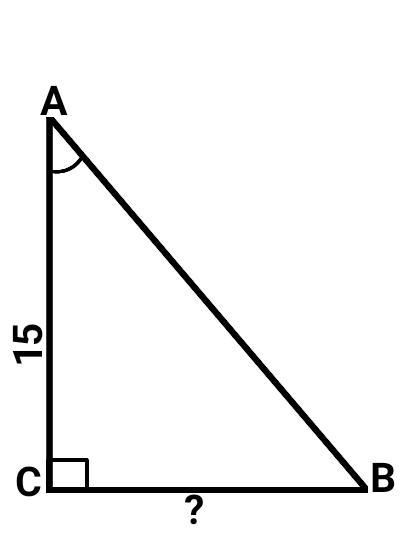
∆АВС — прямоугольный (<С = 90°).
АС = 15.
Tg(<A) = 7/15.
Найти :
ВС = ?
Решение :
Тангенс острого угла прямоугольного треугольника — это отношение противолежащего катета к прилежащему катету.
В нашем случае —
Катет ВС — противолежащий <А.
Катет АС — прилежащий <А.
Тогда по определению —
Tg(<A) = ВС/АС
7/15 = ВС/АС
7/15 = ВС/15
ВС = 7.
Ответ :
7.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: lisukzahar8
Предмет: Математика,
автор: bbakovradmir
Предмет: История,
автор: vasilpolischuk2007
Предмет: Физика,
автор: 1241521
Предмет: Математика,
автор: Volkolak2005