Предмет: Математика,
автор: yuraseven77
Ответ нужен расширенный - с решением.
Приложения:
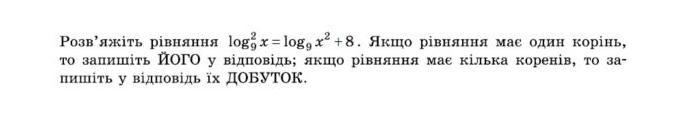
Ответы
Автор ответа:
3
одз:
решаем:
, но так как по одз x>0, то:
продолжаем решать:
делаем замену:
получим квадратное уравнение:
обратная замена:
Данное уравнение имеет два корня.
Произведение:
Ответ: 81
Похожие вопросы
Предмет: Қазақ тiлi,
автор: davidkim2112
Предмет: Алгебра,
автор: vika5822
Предмет: Химия,
автор: ybiicakriperov
Предмет: Алгебра,
автор: baevakatyusha