Предмет: Геометрия,
автор: андрей0123342
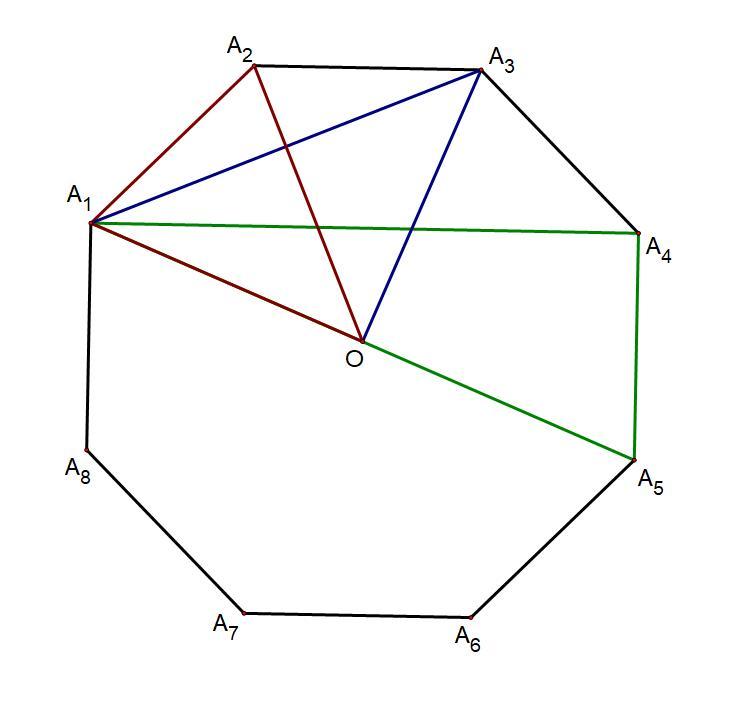
сторона правильного восьмиугольника A1A2A3A4A5A6A7A8 равна 6. найдите диагонали A1A3 A1A4 A1A5
Ответы
Автор ответа:
9
Ответ:
Объяснение:
Пусть O -- центр правильного многоугольника.
Если из точки O провести отрезки OA₁, OA₂,..., ОA₈, то получится 8 равных равнобедренных треугольников (по трём сторонам). Углы при вершинах этих треугольников будут равны и в сумме давать 360°. Тогда:
1.
Рассмотрим ΔOA₁A₂:
A₁A₂ = 6, ∠O = 45°
∠A₁ = ∠A₂ (свойство р/б Δ)
Применим теорему синусов:
2. A₁A₅ = 2A₁O = 2 * 6√2 sin67,5° = 12√2 sin67,5°
3. Рассмотрим ΔA₁A₃O:
∠A₁OA₃ = 2∠A₁OA₂ = 90°
A₁O = OA₃ = 6√2 sin67,5°
В р/б прямоугольном треугольнике гипотенуза равна катету, умноженному на √2, т.е.
A₁A₃ = √2 * 6√2 sin67,5° = 12 sin67,5°
4. Рассмотрим ΔA₁A₄A₅:
A₁A₅ = 12√2 sin67,5°, A₄A₅=6
∠A₁A₄A₅ = 90°
По теореме Пифагора найдём гипотенузу A₁A₄:
Приложения:
helgaaaa20000:
Помоги пожалуйста з заданием по геометрии!!! Очень нужна твоя помощь!!! Прошу!
Помоги пожалуйста з заданием по геометрии!!! Очень нужна твоя помощь!!! Прошу!!!!!!
Похожие вопросы
Предмет: Литература,
автор: rai6412
Предмет: Математика,
автор: matejcuknadia90
Предмет: Математика,
автор: kamillamadarimova
Предмет: Математика,
автор: vipsfsdfsdfsdf
Предмет: Математика,
автор: Аноним