Петя и Вася играют в следующую игру. У них есть шоколадка 2019 × 2020 клеток, и каждым ходом
игрок отламывает от неё прямоугольный кусок и съедает его (в результате остаётся тоже прямоугольник, состоящий из клеток, но меньшего размера). Начинает игру Петя, далее ходят по очереди.
Побеждает тот, после чьего хода периметр шоколадки станет ровно 10. Кто из игроков может выиграть при любой игре соперника? Как ему надо для этого действовать?
Пожалуйста!!!Помогите срочно!!!!!!!!
ДАЮ 25 БАЛЛОВ!!!
Ответы
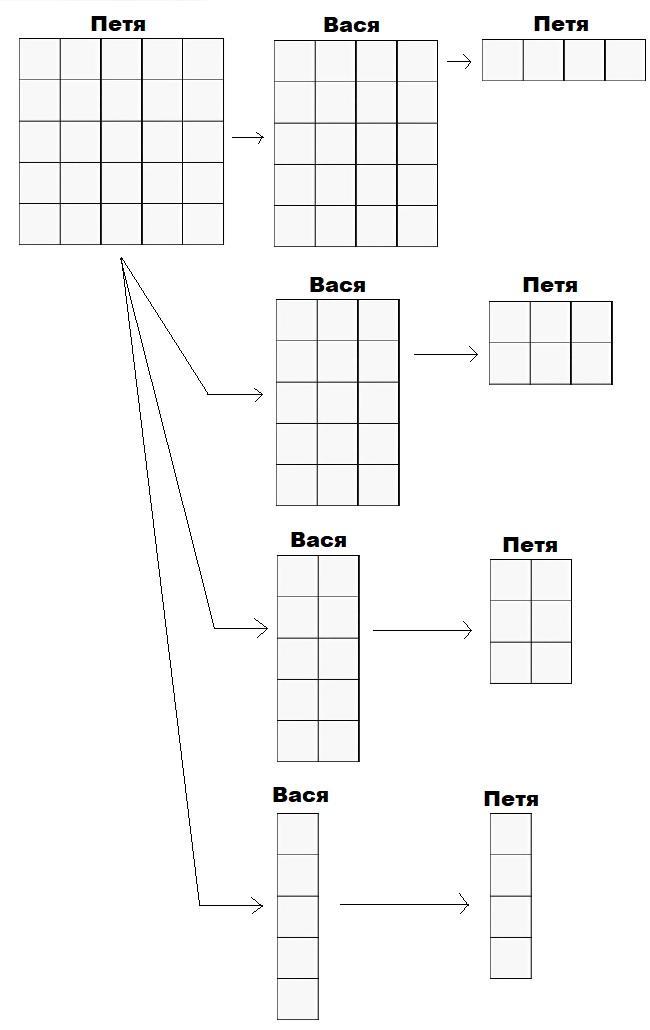
Заметим, что периметр шоколадки станет равным 10, если она будет состоять из прямоугольников 1 x 4 или 2 x 3, т. е. по одной стороне одна клетка, по другой 4 или по одной 2 клетки, по другой 3. По условию Петя начинает игру первый. Покажем, что у него существует выигрышная стратегия. Допустим, что после его очередного хода шоколадка приняла форму квадрата со сторонами 5 x 5. В этом случае, какой бы ход ни сделал Вася, Петя побеждает следующим ходом. Это наглядно показано на рисунке. Следовательно, Петина стратегия заключается в урезании шоколадки на каждом своем ходу до квадрата. На первом ходу он отламывает от шоколадки кусок 1 x 2019, превращая шоколадку в квадрат 2019 x 2019. Затем каждый раз, когда Вася отламывает n клеток по горизонтали, Петя отламывает n клеток по вертикали, превращая шоколадку в квадрат размером (2019-n) x (2019-n). В результате найдется Васин ход, после которого по горизонтали или по вертикали шоколадки останется не более пяти клеток. Следующим своим ходом Петя либо сразу побеждает, если клеток менее пяти, либо урезает шоколадку до квадрата размером 5 x 5, если клеток ровно 5. Далее после любого Васиного хода Петя побеждает согласно рисунку ниже.