Question

Очень СРОЧНО 8КЛАСС


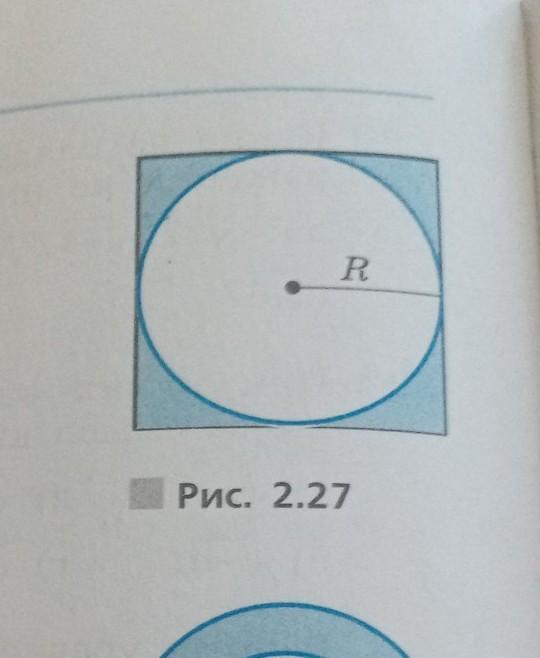
а) Составьте формулу для вычисления площади S закрашенной фигуры. Выразите из этой формулы радиус круга ​

Answer 1

Если представить, что сторона данного квадрата а, то площадь самого квадрата:

$S_{кв} = {a}^{2}$

Площаль окружности вычислим за формулой:

$S_{окр} = \pi {R}^{2}$

Тогда площадь зарисованой фигуры:

$S = S_{кв} - S_{окр} \\S = {a}^{2} - \pi {R}^{2}$

Теперь выразим радиус:

$S = {a}^{2} - \pi {R}^{2} \\ - \pi {R}^{2} = S - {a}^{2} \\ {R}^{2} = \frac{ {a}^{2} - S }{\pi} \\ R = \sqrt{ \frac{ {a}^{2} - S }{\pi}}$

Так как диаметр вписанной в квадрат окружности равен его стороне, то можно записать сторону а как 2R (диаметр). Тогда:

$S = {2R}^{2} - \pi {R}^{2} \\ S = 4{R}^{2} - \pi {R}^{2} \\ S = {R}^{2} (4 - \pi) \\ {R}^{2} = \frac{S}{4 - \pi} \\ R = \sqrt{\frac{S}{4 - \pi}}$

Answer 2

Ответ:R=√S/(4-π)

Объяснение:

Описанная фигура - квадрат со стороной 2R⇒ S1=(2*R)²=4*R²

S2=π*R²- площадь круга ,

Площадь закрашенной фигуры  найдем как разность площади

квадрата и площади круга

S=S1-S2=4*R²-π*R²=R²*(4-π)

S=R²*(4-π)

Выразим R

R²*(4-π)=S

R²=S/(4-π)

R=±√S/(4-π)

Так как  R - радиус, то R>0⇒

R=√S/(4-π)

Ответ:R=√S/(4-π)