Предмет: Геометрия,
автор: alinmalina1278
найдите диаметр окружности если его концы удалены от некоторой касательной на 15 см и 19 см
Ответы
Автор ответа:
2
Ответ: 34 см
Объяснение:
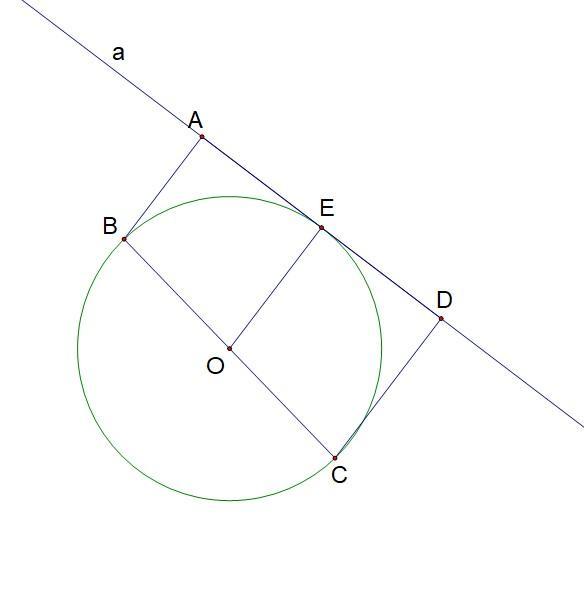
1. Расстояния от концов диаметра до касательной -- это перпендикуляры к касательной из этих концов.
AB = 15 см, CD = 19 см
2. O - центр окружности, E - точка касания. Проведём OE. По свойству касательной к окружности OE ⊥ AD
3. Так как OE ⊥ AD, AB ⊥ AD, CD ⊥ AD, то AB ║ CD ║ OE
4. AB║CD ⇒ ABCD - трапеция
5. BO = OC, AB║CD║OE ⇒ AE = ED (теорема Фалеса)
6. Из пункта 5 следует, что OE - средняя линия трапеции ABCD.
OE = (AB + CD)/2 = (15+19)/2 = 34/2 = 17 см
7. OE - радиус. Тогда диаметр BC = 2OE = 2*17 = 34 см
Приложения:
Похожие вопросы
Предмет: История,
автор: krushan1102
Предмет: Физика,
автор: lotsamartem0
Предмет: История,
автор: sa9n
Предмет: Математика,
автор: каролина136в
Предмет: Литература,
автор: kripersuper516