Question

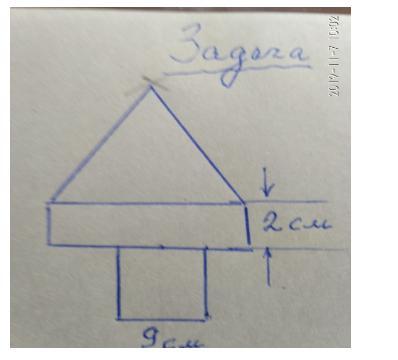
На рисунку 1 зображена вежа, яка складається з квадрату, прямокутника й рiвностороннього
трикутника. Вiдомо, що периметри всiх трьох фiгур рiвнi. Сторона квадрату – 9 см. Знайти ширину
прямокутника. Рис. 1: до задачi 2
№2
Є три числа. Вiдомо, що добуток першого числа та другого закiнчується нулем, а добуток
першого числа та третього й добуток другого числа та третього не закiнчуються нулем. Чи може сума
всiх трьох чисел закiнчуватися на 3 ?

Answer 1

Ответ:

№1. Условие задачи неправильно!

№2. Не может

Пошаговое объяснение:

№1. Определим периметр квадрата: Р=4·а=4·9 = 36 см.

Пусть ширина прямоугольника равна х. Тогда периметр прямоугольника Р=2·(х+2).

По условию периметры всех фигур равны, отсюда

2·(х+2)=36

х+2=18

х=18-2=16 см.

С другой стороны: периметр равностороннего треугольника равен Р=3·х = 36 или х= 12 см.

Отсюда заключаем, что условие задачи неправильно!

№2. Пусть a, b и c числа из условия задачи. По условию:

a·b=...0

a·c≠...0

b·c≠...0

Из двух последних неравенств заключаем, что ни одна из этих чисел не оканчивается на 0!

Тогда из a·b=...0 заключаем, что a или b оканчивается на 5, а другой оканчивается на цифры 2 или 4 или 6 или 8. Пусть, для определённости, a оканчивается на 5, b оканчивается на цифры 2 или 4 или 6 или 8.

Тогда из-за условия a·c≠...0 число c не может оканчиваться на цифры 2 или 4 или 6 или 8.

Теперь рассмотрим их сумму

1) если b=...2: a+b+c=...5+...2+c=...7+c=...3 и c=...3-...7=...6, что не может быть;

2) если b=...4: a+b+c=...5+...4+c=...9+c=...3 и c=...3-...9=...4, что не может быть;

3) если b=...6: a+b+c=...5+...6+c=...1+c=...3 и c=...3-...1=...2, что не может быть;

4) если b=...8: a+b+c=...5+...8+c=...3+c=...3 и c=...3-...3=...0, что не может быть.

Ответ: не может.