Предмет: Математика,
автор: 61dikterev16
Найдите наименьшее натуральное значение числа x, для которого существует целое y такое, что выполняется равенство xy−4x+5y=547.
Ответы
Автор ответа:
1
xy-4x+5y = 547.
x(y-4) + 5y = 547
x = (547-5y)/(y-4) Выделим целую часть (во вложении)
x = -5 + (527/(y-4) ) .527 нацело делится на 31,17,1,527. Т.к. x - натурально число ,то 527/(y-4) > 0 . y-4 = 31 или y - 4 = 17 или y -4 = 1 или y-4 = 527. y-4= 527 не подходит (x<0) . Чтобы 527/(y-4) было минимально ,нужно чтобы y-4 был максимальным ) ,это происходит при y-4 = 31.тогда x = -5+(527/31) = 12
Ответ :12
Приложения:
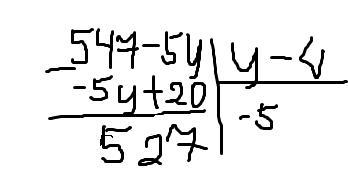
Похожие вопросы
Предмет: Українська література,
автор: foxdoshik
Предмет: Английский язык,
автор: ilaluckin13
Предмет: Английский язык,
автор: Мишкабаянов
Предмет: Алгебра,
автор: Аноним