Предмет: Алгебра,
автор: dasew12
Помогите пожалуйста
Приложения:
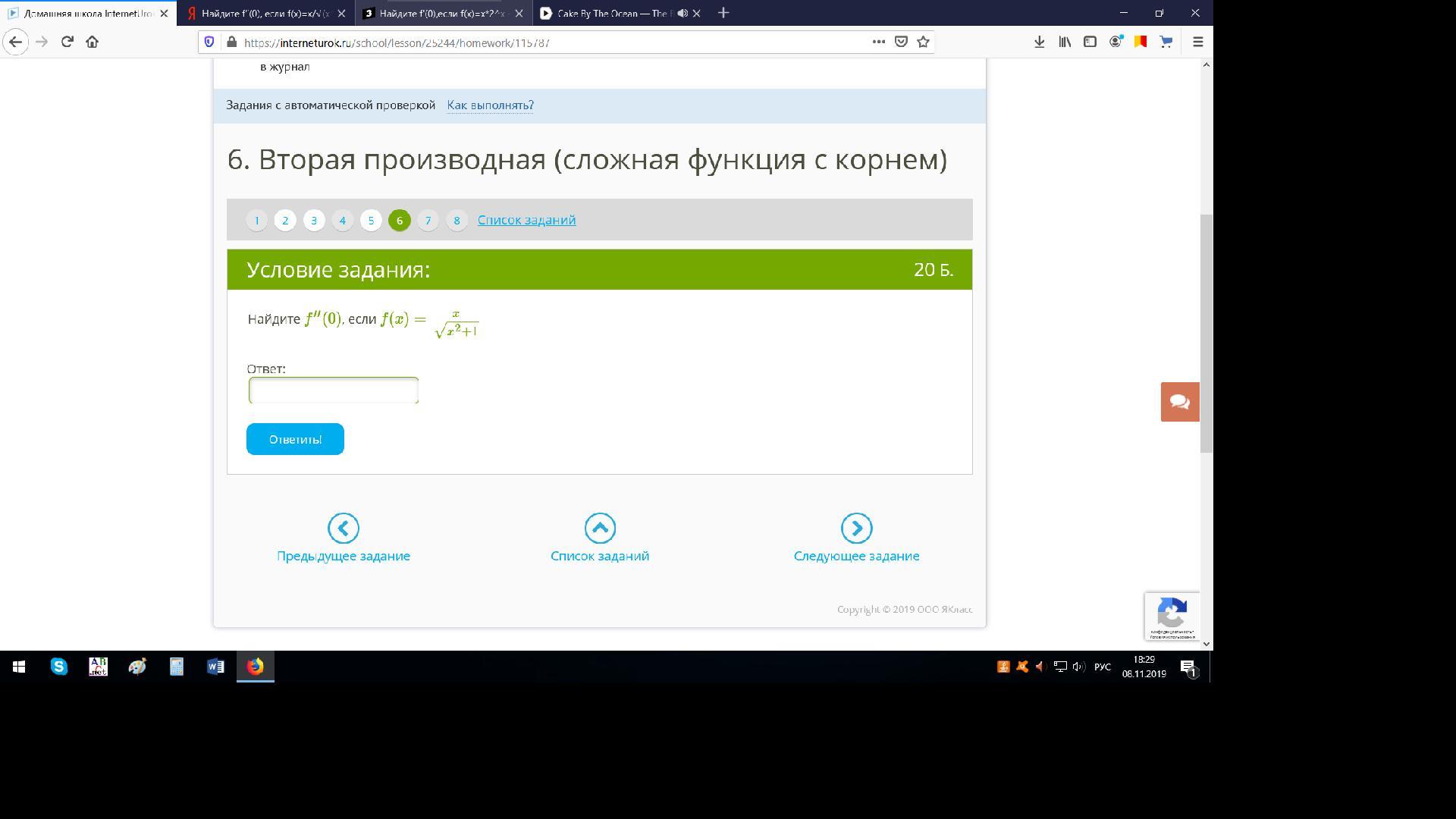
Ответы
Автор ответа:
1
NNNLLL54:
(sqrtu)'=1/(2sqrtu) , (1/u)'= -(u'/u^2)
Похожие вопросы
Предмет: Математика,
автор: Varvarky
Предмет: Литература,
автор: rinakovachuk110
Предмет: Українська мова,
автор: ksenzovaevelina
Предмет: Математика,
автор: DILLISA
Предмет: Физика,
автор: mikin75