Предмет: Алгебра,
автор: mILEENNSSSSSS7
решите пожалуйста пределы
Приложения:
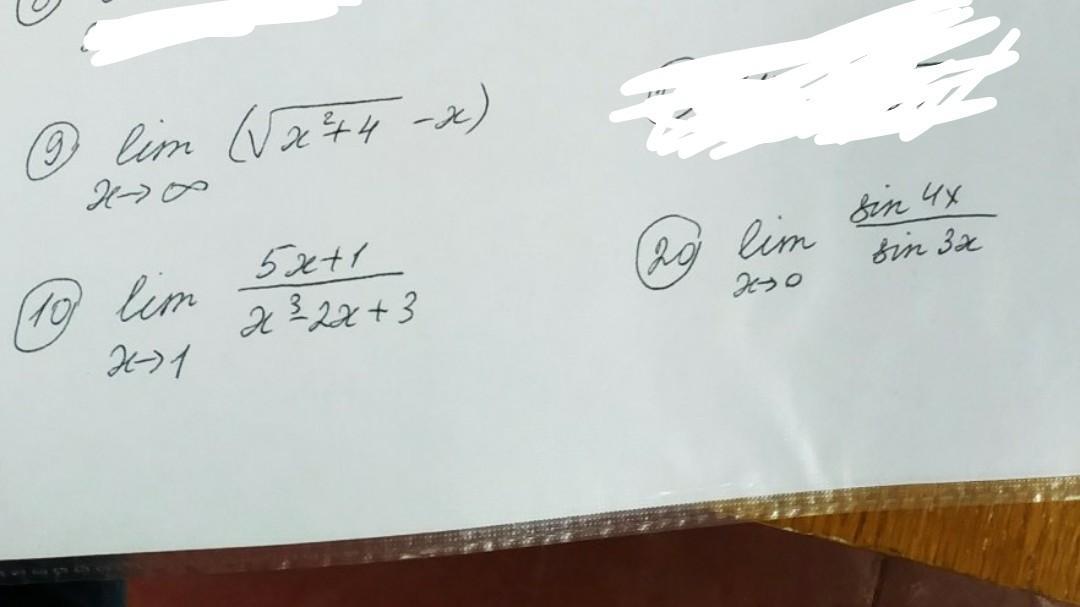
Ответы
Автор ответа:
1
Автор ответа:
0
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Биология,
автор: annamarcenkozilskaa
Предмет: Алгебра,
автор: kamillaiskildina906
Предмет: Химия,
автор: kolomiets12021202
Предмет: Алгебра,
автор: лера1329
Предмет: Информатика,
автор: elizavetavoron2