Предмет: Математика,
автор: KatherinePirs
Помогите с пределами
Приложения:
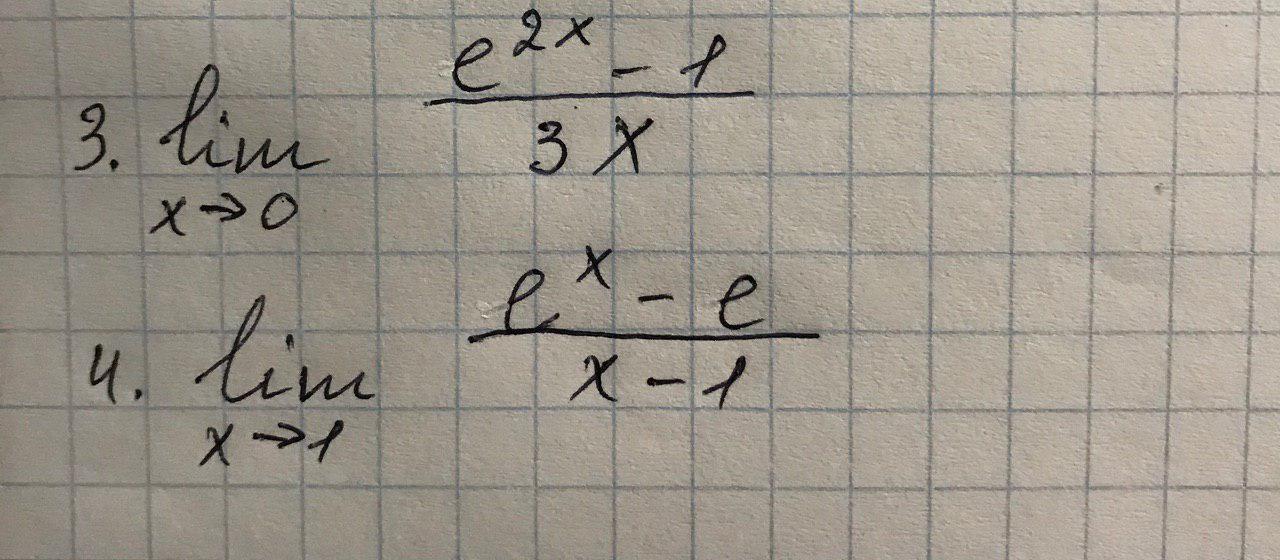
Ответы
Автор ответа:
1
Применим правило Лопиталя:
Применим правило Лопиталя:
Похожие вопросы
Предмет: Алгебра,
автор: Mansur070809010
Предмет: История,
автор: bukhonin0971
Предмет: Қазақ тiлi,
автор: mikego7ytz
Предмет: Математика,
автор: sveta22885