Предмет: Алгебра,
автор: maxnikit03
Производные элементарных функций. Часть 4
Приложения:
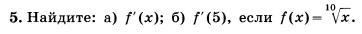
Ответы
Автор ответа:
0
Дана функция
Найдём её производную:
Теперь находим значение производной в точке 5:
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: namvadim98
Предмет: Математика,
автор: nataliakurbonova936
Предмет: Алгебра,
автор: arslankumarov69
Предмет: Математика,
автор: влад1483
Предмет: Литература,
автор: Bfdcbh