Question

Решите уравнение 9x^4+6x^3-14x^2+x+2=0

Answer 1

Воспользовался Схемой Горнера

Answer 2

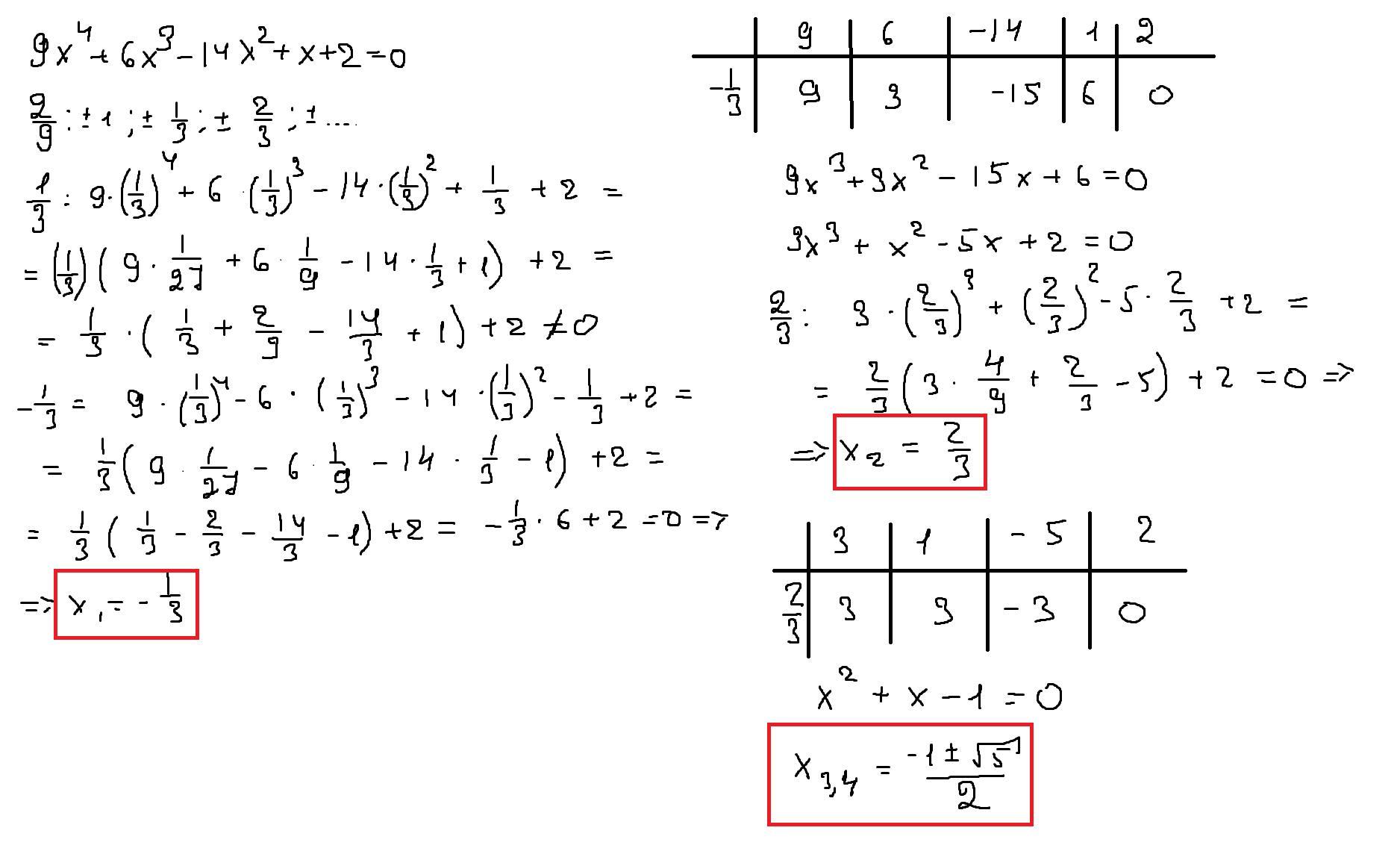
Итак, дано уравнение $9x^4+6x^3-14x^2+x+2=0$

Это уравнение высокого порядка, следовательно, каких-то методов решения в общем виде особо и нет. Поэтому надо что-то придумывать.

Из следствия теоремы Безу, если у такого уравнения, как наше, есть целые корни, то это делители свободного члена.

Сумма коэффициентов не равна 0, значит, х=1 - не корень.

Суммы коэффициентов при четных и нечетных степенях не равны, поэтому х=-1 - не корень. Подставив 2 и -2 в исходное уравнение, убеждаемся, что равенство не выполняется, а значит, у нашего уравнения нет целых корней. Что можно сделать в таком случае?

Как вообще можно получить многочлен четвертой степени? Можно, например, перемножить два квадратных трехчлена. Учитывая, что коэффициент при старшей степени равен 9, попробуем в каждой скобке при квадрате поставить 3 (3*3=9). Тогда получим

$(3x^2+ax+b)(3x^2+cx+d)$

Вообще я сейчас применяю метод неопределенных коэффициентов. Раскрыв скобки, мы получим большое выражение, взяв коэффициенты из нашего исходного выражения мы получим систему, решив которую получим коэффициенты нужного нам разложения.

$(3x^2+ax+b)(3x^2+cx+d)=\\=9x^4+3cx^3+3dx^2+3ax^3+acx^2+adx+3bx^2+bcx+bd=\\=9x^4+(3c+3a)x^3+(3d+ac+3b)x^2+(ab+bc)x+bd=\\=9x^4+6x^3-14x^2+x+2$

Думаю, понятно, откуда система возьмется. Просто при каждой степени приравниваем буквенное выражение к коэффициенту из нашего исходного многочлена. Так как эти условия должны выполняться одновременно, то это будет именно система, а не совокупность.

$\begin{Bmatrix} 3c+3a=6 \\ 3d+ac+3b=-14\\ ad+bc=1\\ bd=2 \end{matrix}$

Итак, есть система

$\begin{Bmatrix} a+c=2 \\ 3b+3d+ac=-14\\ ad+bc=1\\ bd=2 \end{matrix}$

Решить её полностью будет сложно, нам нужно хотя бы 1 решение.

Попробуем его подобрать, причем постараемся взять как можно больше целых чисел. a=0, c=2 и a=2, c=0 не подойдут, так как тогда по второму уравнение сумма b и d равна -14/3, но решая 3-е и 4-е уравнения, там одно число будет целым, а у второго знаменатель 2, так что не выполняется. Попробуем взять $a=-1; \; c=3$

Подставляем в 3-е и 4-е уравнения

$\left \{ {{-d+3b=1} \atop {d=\frac{2}{b} }} \right. ;\left \{ {{3b-\frac{2}{b}-1=0 } \atop {d=\frac{2}{b} }} \right. ; \left \{ {{\frac{3b^2-b-2}{b}=0 } \atop {d=\frac{2}{b} }} \right. ;$

Квадратное уравнение в числителе легко решается, так как там сумма коэффициентов равна 0, то есть

$\left [ {{b=1} \atop {b=\frac{c}{a}=-\frac{2}{3}  }} \right.$

К сожалению, взять $b=1 \Rightarrow d=2$ не получится, так как тогда все коэффициенты целые, а значит, второе уравнение автоматически не выполнится.

Значит, получаем

$\left \{ {{b=-\frac{2}{3} } \atop {d=\frac{2}{b} =\frac{2}{-\frac{2}{3} }=-3 }} \right.$

Проверим эти значения на 2-м уравнении.

$ac+3b+3d=-14: (-1)\cdot 3+3\cdot \bigg(-\frac{2}{3} \bigg)+3\cdot (-3)=-14$

$-3-2-9=-14; -14=-14$

Верно, то есть мы получили те самые коэффициенты разложения

$\begin{Bmatrix} a=-1 \\ b=-\frac{2}{3} \\ c=3\\ d=-3 \end{matrix}$

То есть $9x^4+6x^3-14x^2+x+2=$

$=\bigg(3x^2-x-\frac{2}{3} \bigg)(3x^2+3x-3)=0$

$\left [ {{3x^2-x-\frac{2}{3}=0 \: \bigg | \cdot 3 } \atop {3x^2+3x-3=0 \: \bigg | \div 3 }} \right. \Rightarrow \left [ {{9x^2-3x-2=0 \: \: \: (1)} \atop {x^2+x-1=0 \: \: \: \: \: \: \: \: (2) }} \right.$

Решаем каждое уравнение:

$(1): 9x^2-3x-2=0; D=(-3)^2-4\cdot 9 \cdot (-2)=9+72=81=9^2$

$x_{1,2}=\frac{3\pm 9}{18}; x_1=-\frac{6}{18}=-\frac{1}{3}; \: x_2=\frac{12}{18}=\frac{2}{3}$

$(2): x^2+x-1=0; D=1-4\cdot 1 \cdot (-1)=5; \: x_{3,4}=\frac{-1\pm \sqrt{5} }{2}$

В принципе, упорядочивать корни необязательно, так что так и оставим.

Ответ: $\boxed{-\frac{1}{3}; \frac{2}{3};  \frac{-1\pm \sqrt{5} }{2}  }$