Два мотылька — большой и маленький — летают вокруг фонаря по круговым траекториям, лежащим в одной плоскости. Радиус «орбиты» большого в 2 раза больше, чем радиус орбиты маленького. При этом период движения большого мотылька Tb=9 с, а период движения маленького Ts=4 с. В некоторый момент времени мотыльки оказались на минимальном возможном (для этих траекторий) расстоянии друг от друга. Во сколько раз увеличится это расстояние к моменту времени t=6 с? Ответ запишите в виде десятичной дроби с округлением до сотых
Ответы
Ответ:
Расстояние увеличится в 1,73 раза.
Пошаговое объяснение:
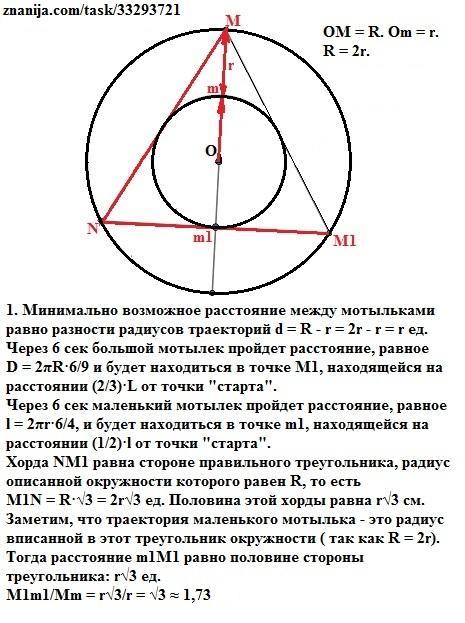
Минимально возможное расстояние между мотыльками равно разности радиусов траекторий d = R - r = 2r - r = r ед.
Через 6 сек большой мотылек пройдет расстояние, равное
D = 2πR·6/9 и будет находиться в точке М1, находящейся на расстоянии (2/3)·L от точки "старта".
Через 6 сек маленький мотылек пройдет расстояние, равное
l = 2πr·6/4, и будет находиться в точке m1, находящейся на расстоянии (1/2)·l от точки "старта".
Хорда NM1 равна стороне правильного треугольника, радиус описанной окружности которого равен R, то есть
M1N = R·√3 = 2r√3 ед. Половина этой хорды равна r√3 см.
Заметим, что траектория маленького мотылька - это радиус вписанной в этот треугольник окружности ( так как R = 2r).
Тогда расстояние m1M1 равно половине стороны треугольника:
M1m1 = r√3 ед.
Отношение расстояний: M1m1/Mm = r√3/r = √3 ≈ 1,73.