Предмет: Алгебра,
автор: yuoldtpemyik
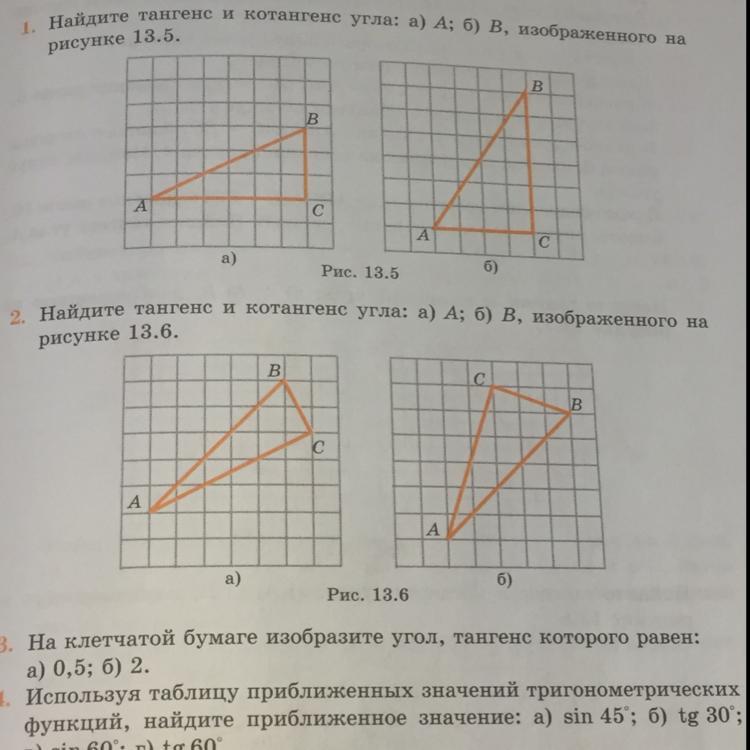
найдите тангенс и котангенс угла: а) А; б) В, изображенного на рисунке 13.6
Приложения:
Ответы
Автор ответа:
80
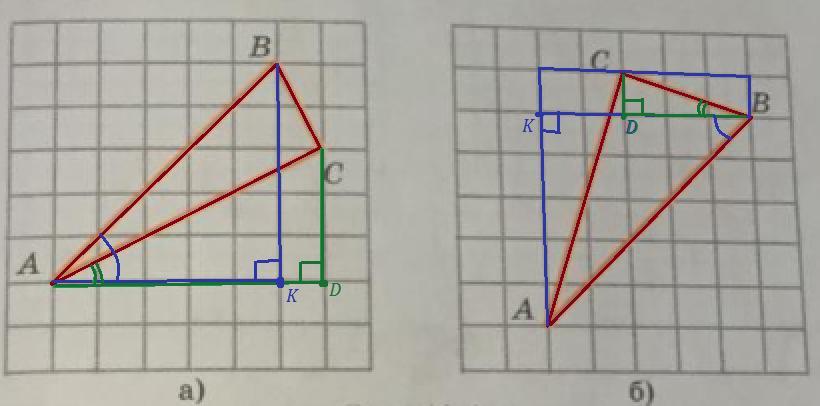
Тангенс угла в прямоугольном треугольнике - это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
Смотри рисунок.
Приложения:
Похожие вопросы
Предмет: История,
автор: sojedu
Предмет: Литература,
автор: arsenykudanov4
Предмет: История,
автор: koptevam2010
Предмет: Алгебра,
автор: mabnesss5
Предмет: Математика,
автор: лучшийученик3