Предмет: Алгебра, автор: zaya9ku

Помогите решить систему ур-ий пожалуйста

Приложения:

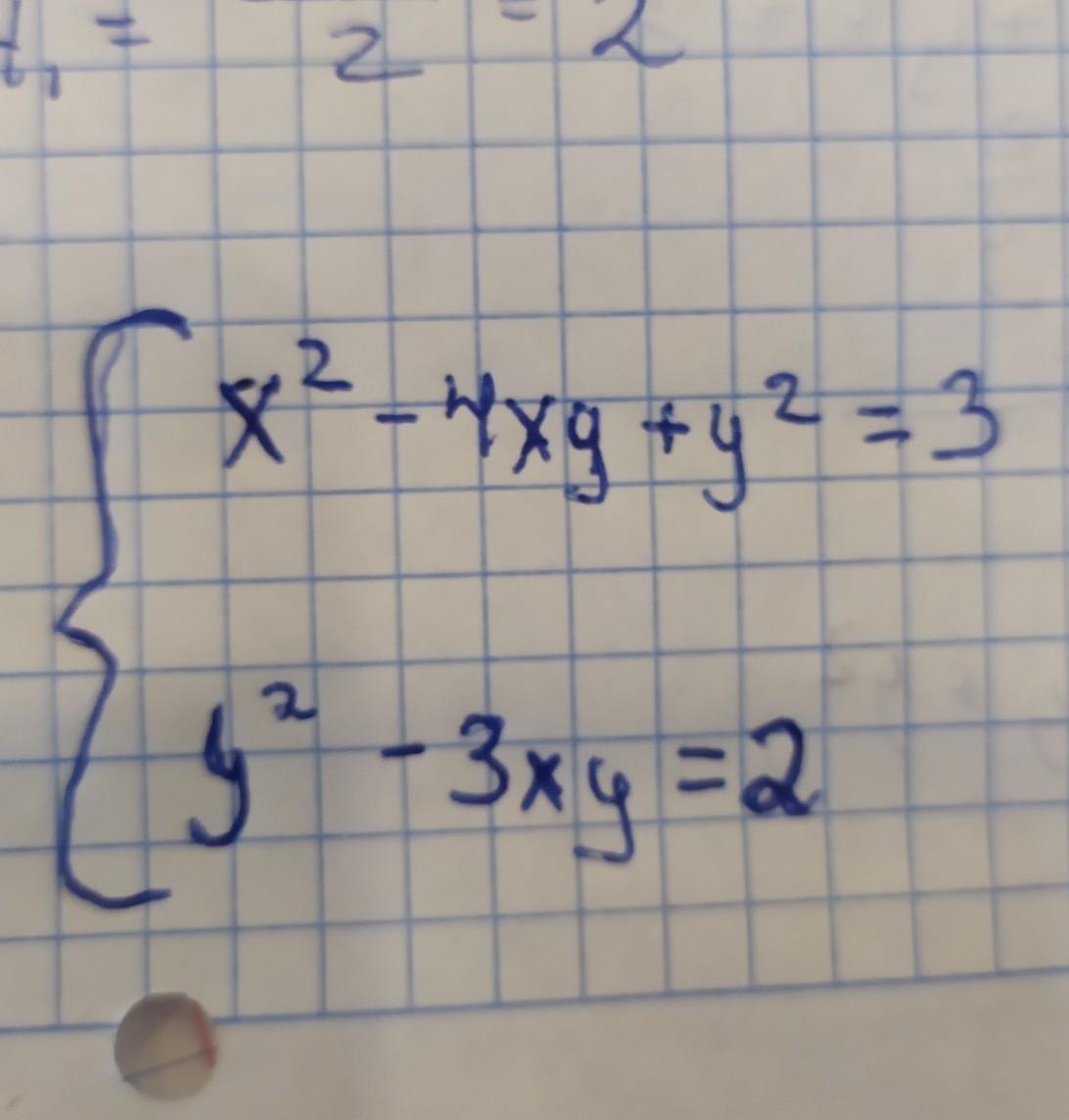
zaya9ku: не знаю правильно ли я решил, но решив через у/х, у меня получилось, что у=2х, поставив во второе ур-ие, получил что х^2=-1

zaya9ku: значит оно не имеет корней?

zaya9ku: ведь всегда при возведении в квадрат число положительное

zaya9ku: а понял

zaya9ku: получив что y=-x, поставив во второе, получил x= корню из 1/2, а у = минус корню из 1/2

zaya9ku: просто из начально забыл про второй корень при y/x там получил 2 и - 1

zaya9ku: все подставил, и сошлось в проверке

zaya9ku: спасибо большущее))

NNNLLL54: :))) ну вот, так решаются системы, которые можно привести к системе, где одно из уравнений будет однородным. Главное получить уравнение , в правой части которого есть 0, а в левой части сумма показателей степеней - одно и то же число k( в данном примере k=2).

zaya9ku: хорошо)

Ответы

Автор ответа: NNNLLL54

$\left \{ {{x^2-4xy+y^2=3} \atop {y^2-3xy=2}} \right.\; \; \left \{ {{x^2-xy+(y^2-3xy)=3} \atop {y^2-3xy=2}} \right.\; \; \left \{ {{x^2-xy+2=3} \atop {y^2-3xy=2}} \right.\; \; \left \{ {{x^2-xy=1\; |\cdot (-2)} \atop {y^2-3xy=2\qquad }} \right. \oplus \\\\\left \{ {{-2x^2-xy+y^2=0} \atop {y^2-3xy=2\quad }} \right. \; \; \left \{ {{2x^2-xy-y^2=0} \atop {y^2-3xy=2\; \; \; }} \right. \\\\2x^2-xy-y^2=0\; |:y^2\ne 0\\\\(\esli\; \; y=0\; ,\; to\; \; y^2-3xy=0\ne 2\; \; \to \; \; y=0\; ne\; koren\; yravneniya\; )$

$2\cdot (\frac{x}{y})^2+\frac{x}{y}-1=0\; \; ,\; \; t=\frac{x}{y}\\\\2t^2+t-1=0\; \; ,\; \; D=9\; \; ,\; \; t_1=\frac{-1+3}{4}=\frac{1}{2}\; \; ,\; \; t_2=\frac{-1-3}{4}=-1\\\\a)\; \; \frac{x}{y}=\frac{1}{2}\; \; \to \; \; y=2x\; ,\\\\y^2-3xy=4x^2-6x^2=-2x^2\; \; ,\; \; -2x^2=2\; ,\; \; x^2=-1\; \; \to \; \; x\in \varnothing \\\\net\; reshenij\\\\b)\; \; \frac{x}{y}=-1\; \; \to \; \; y=-x\; ,\\\\y^2-3xy=x^2+3x^2=4x^2\; \; ,\; \; 4x^2=2\; \; ,\; x^2=\frac{1}{4}\; \; ,\; \; x=\pm \frac{1}{\sqrt2}\; ,\\\\y=-x=\mp \frac{1}{\sqrt2}\\\\Otvet:\; \; (-\frac{1}{\sqrt2}\; ,\; \frac{1}{\sqrt2})\; \; ,\; \; (\frac{1}{\sqrt2}\; ,\; -\frac{1}{\sqrt2})\; .$