Предмет: Алгебра,
автор: yasyapotapova7
Умоляю
Должен получиться 1
Приложения:
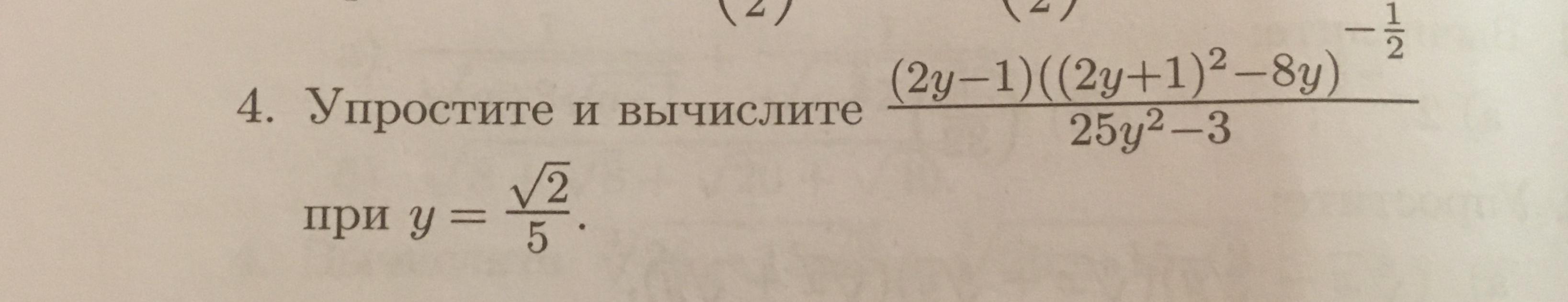
Tanda80:
-1/2 - это показатель степени?
Да
Ответы
Автор ответа:
0
При у=√2/5
а значит
Таким образом,
Подставляя у=√2/5 получаем:
Похожие вопросы
Предмет: Литература,
автор: Negrs228
Предмет: Русский язык,
автор: vikazvereva18062000
Предмет: Математика,
автор: evaporate65
Предмет: Литература,
автор: tamaraashirova