Предмет: Алгебра,
автор: Аноним
ПОМОГИТЕ УПРОСТИТЬ ВЫРАЖЕНИЕ ПО ЛОГАРИФМАМ СРОЧНО
Приложения:
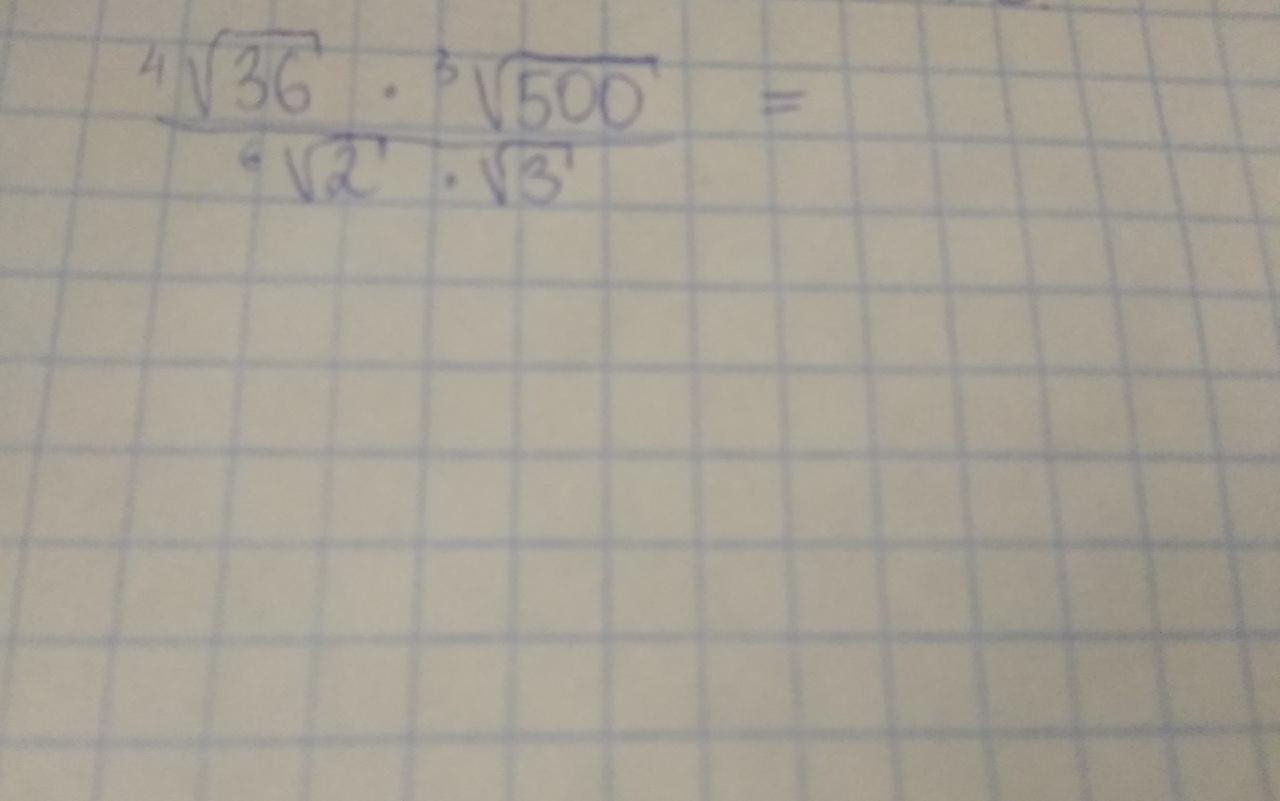
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Физика,
автор: aleksyyy13
Предмет: Українська література,
автор: avramovadasha2708
Предмет: Русский язык,
автор: bastettn
Предмет: Математика,
автор: Виола1506
Предмет: Математика,
автор: pilyugina1984