Предмет: Алгебра,
автор: d1agnoz
Как решить уравнение:
(sinx)^2–(sin2x)^2+(sin3x)^2=1/2
Приложения:
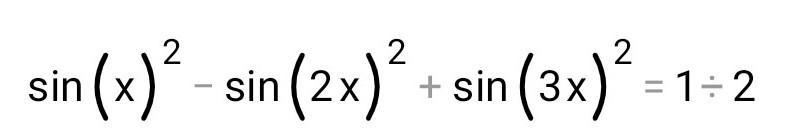
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: untulovavalentina
Предмет: Геометрия,
автор: Necessar
Предмет: Физика,
автор: dimson4600
Предмет: Математика,
автор: саша3078