Question

Ребят, помогите с решением, пожалуйста.

Answer 1

Найти Фокусы и эксцентриситет гиперболы

Каноническое уравнение гиперболы имеет вид

$\displaystyle  \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

где a.b  – положительные действительные числа.

Выполним преобразование:

$\displaystyle  x^2-4y^2=16\\\\\frac{x^2}{16}-\frac{4y^2}{16}=1\\\\\frac{x^2}{4^2}-\frac{y^2}{2^2}=1$

Фокусы:

расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле:

c=√(a²+b²)

И, соответственно, фокусы имеют координаты: F₁(c;0) и F₂(-c;0) .

Найдем расстояние

$\displaystyle  c=\sqrt{4^2+2^2}=\sqrt{20} =2\sqrt{5}$

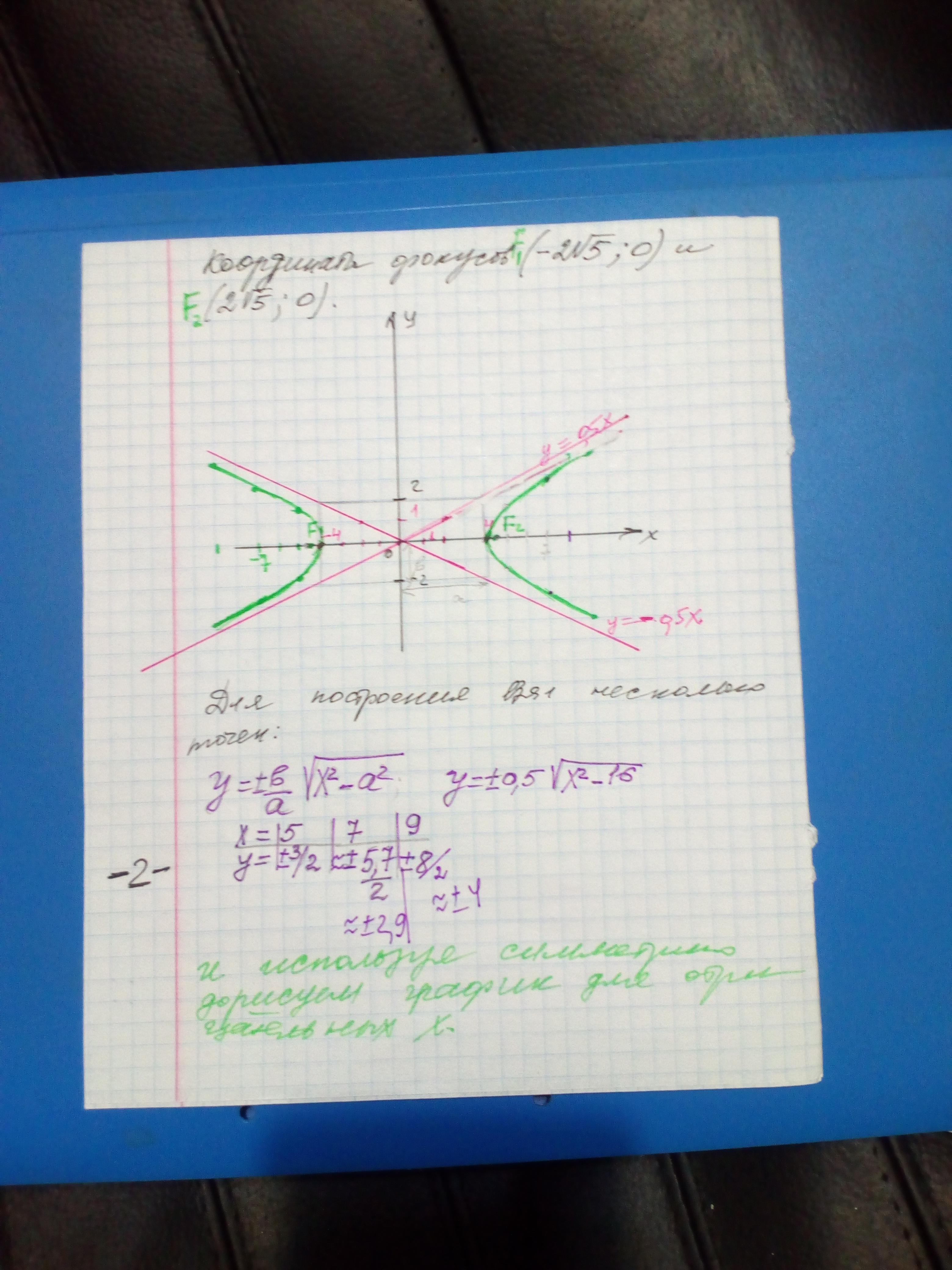
Тогда координаты Фокусов F₁(2√5;0) и F₂(-2√5;0)

Эксцентриситет

Эксцентриситетом гиперболы называют отношение ε=с/а

ε=2√5 / 4 = √5/2

Для чего нужен эксцентриситет?

При увеличении эксцентриситета т.е. ε→∞ ветви гиперболы «распрямляются» к оси .

Если же значение эксцентриситета приближается к единице, то ветви гиперболы «сплющиваются» к оси Ох .

Для построения графика:

1) Найдем вешины гиперболы

y=0 тогда x²/4²=1 отсюда x²=16 и Вершины в точках (4;0) и (-4;0)

2) Найдем асимптоты

y=(b/a)x и y=(-b/a)x

y=1/2*x и y= - 1/2*x

3) Дополнительные точки

4y²=x²-16

y²=(x²-16)/4

y=±√(x²-16)/4

х=5 тогда у= ±1,5

График в приложении

Answer 2

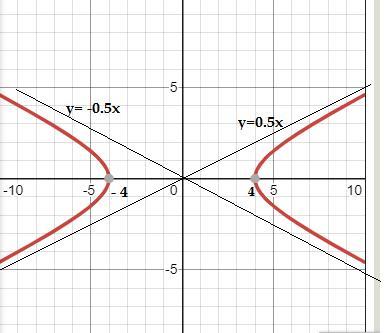
Ответ: во вложении Объяснение: