Предмет: Алгебра,
автор: alex230132
Не могу понять, как расписать числитель)
Приложения:
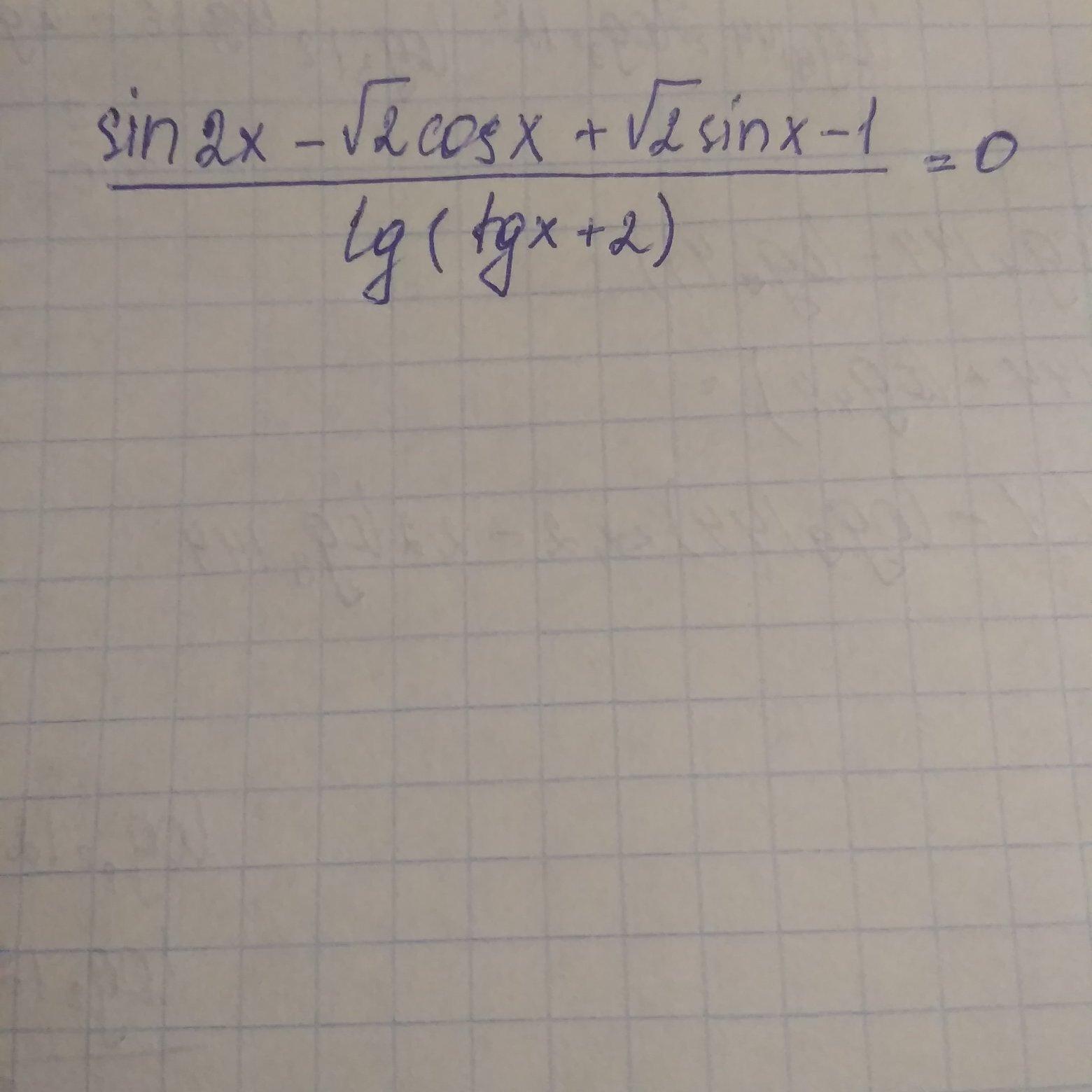
artalex74:
(первое и последнее) и (второе и третье) слагаемые. затем завершите разложение на множители
Ответы
Автор ответа:
1
ОДЗ:x∈()\{
}
С учётом нашего ОДЗ получается только один корень
k∈Z
Похожие вопросы
Предмет: Русский язык,
автор: sundetovbatyr0
Предмет: Геометрия,
автор: solomiamalovana1
Предмет: Русский язык,
автор: madinagapbaeva291
Предмет: Биология,
автор: Аноним