Предмет: Алгебра,
автор: habirov71
Написать уравнение касательной к графику функции y=x^3 − 4 x в точке с абсциссой x0=2
Ответы
Автор ответа:
1
Дано: F(x)= x³ - 4*x - функция, Хо = 2.
Найти: Уравнение касательной.
Решение.
Y = F'(Xo)*(x - Xo) + F(Xo) - формула касательной.
Находим первую производную - k - наклон касательной.
F'(x) = 3 *x² - 4.
Вычисляем в точке Хо = 2.
F'(2) = 12 - 4 = 8 - производная
F(2) = 8 + 0 + -8 + 0 = 0 - функция.
Записываем уравнения прямой.
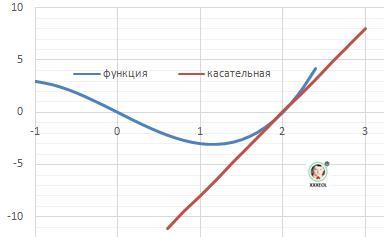
Y = 8*(x - 2) + (0) = 8*x - 16 - уравнение касательной - ОТВЕТ
Рисунок к задаче в приложении.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: bashirovamadina08
Предмет: Английский язык,
автор: saparovaolesa414
Предмет: Алгебра,
автор: kkrek
Предмет: Математика,
автор: alina1170
Предмет: Литература,
автор: Crafak