Прямая задана общим уравнением. Написать ее каноническое и параметрическое уравнение
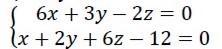
Ответы
Чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей.
Пусть z = 0 , тогда получаем систему двух линейных уравнений с двумя неизвестными: 6x + 3y = 0
x + 2y - 12 = 0. Умножим это уравнение на -6.
6x + 3y = 0
-6x - 12y +72 = 0
Почленно складываем уравнения и находим решение системы:
-9y = -72, y = -72/-9 = 8. Подставим в первое уравнение.
x = 12 - 2y = 12 - 2*8 = 12 - 16 = -4.
Получили точку на заданной прямой: (-4; 8; 0).
Находим направляющий вектор прямой как результат векторного умножения нормальных векторов заданных плоскостей.
i j k | i j
6 3 -2 | 6 3
1 2 6 | 1 2. Применим треугольную схему.
18i - 2j + 12 k - 36j + 4i - 3k = 22i - 38j + 9k.
Направляющий вектор равен (22; -38; 9).
Теперь можно составить каноническое уравнение прямой.
(x + 4)/22 = (y - 8)/(-38) = z/9.
Если каждый член этого уравнения приравнять t, то получим параметрические уравнения прямой.
{x = 22t - 4,
{y = -38y + 8,
{ z = 9t.