Предмет: Математика,
автор: DoctorWhoFan
Длины сторон прямоугольника являются корнями данного уравнения. Чему равен его периметр?
Приложения:
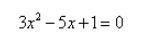
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Биология,
автор: lajf6526
Предмет: Математика,
автор: elisey3736
Предмет: Геометрия,
автор: teyyii2704
Предмет: Алгебра,
автор: VEPRb
Предмет: Математика,
автор: ира743