Предмет: Алгебра,
автор: kott5
Срочно!!! ПОМОГИТЕ, очень нужно
Приложения:
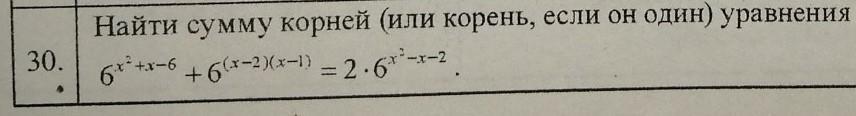
Ответы
Автор ответа:
1
Ответ:
2
Объяснение:
разложим многочлены на множители:
корни по теореме Виета x1=-3,x2=2
корни по теореме Виета x1=-1,x2=2
так как
подставляя в уравнение и сокращая на y^x, получаем биквадратное уравнение
откуда
y1=1; y2=-1
только первый корень удовлетворяет условию y>0, значит
откуда x-2=0; x=2
Похожие вопросы
Предмет: Математика,
автор: anadolskaaliza
Предмет: История,
автор: bestgamerdud
Предмет: История,
автор: Hazik228
Предмет: География,
автор: Василиска844
Предмет: Алгебра,
автор: сабрина74